Потенциальные течения

Как было указано, течение, признаком кото­рого является условие 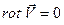, называется потенциальным (безвихревым). В са­мом деле, можно ввести в рассмотрение скалярную функцию 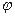та­кую, что

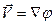(2.89)

и условие отсутствия завихренности будет выполняться автоматиче­ски.

Здесь функция 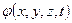носит название потенциала скорости, почему и течения рассматриваемого типа называются потенциальными.

В уравнениях движения Громеки -Лэмба член, содержащий в явном виде 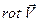, исчезает. Система уравнений движения приобре­тает вид

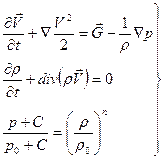(2.90)

В потенциальном поле массовых сил П сразу получаем

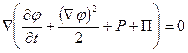
и далее

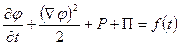, (2.91)

где П и Р имеют тот же смысл, что и в интеграле Бернулли.

Полученный интеграл носит название интеграла Коши-Лагранжа. В отличие от интеграла Бернулли, он распространя­ется и на случай нестационарных течений. Но, с другой стороны, интеграл Коши - Лагранжа пригоден лишь для безвихревых течений.

В случае несжимаемой жидкости

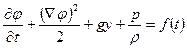, (2.92)

где функция f(t) может быть выражена через известные параметры течения в какой-либо точке потока.

На свободной поверхности динамическое условие требует равенства давления жидкости давлению газовой атмосферы р _г. В соответствии с интегралом Коши - Лагранжа на свободной границе должно выполняться

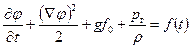(2.93)

Функцию f(t) можно определить, например, из рассмотрения ус­ловий в бесконечно удаленной точке, где 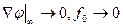, а 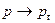. Тогда 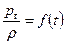, и динамическое условие на свободной границе примет вид

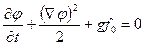(2.94)

Таким образом, общая задача о потенциальных течениях иде­альной несжимаемой жидкости распадается на две. Сначала реша­ется кинематическая часть задачи, посвященная нахождению по­тенциала скорости 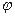на основе решения уравнения Лапласа. Затем решается динамическая часть задачи путем вычисления давления из уравнения Коши - Лагранжа по известным значениям потенциала скорости.