Интеграл Бернулли

Придадим уравнению количества движения иную форму. Для этого воспользуемся известной формулой вектор­ного анализа

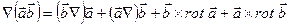
положив в ней 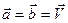. Следовательно, справедливо равенство

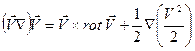
Таким образом, уравнение количества движения приобретет вид уравнения Громеки – Лэмба

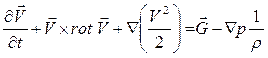(2.79)

Как мы убедимся в дальнейшем, эта форма уравнения чрезвы­чайно удобна для анализа течения идеальной жидкости.

Рассмотрим сначала случай стационарного течения, т. е. поло­жим 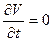, и умножим (2.48) скалярно на вектор 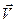. Тогда по­лучим

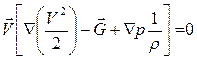(2.80)

Так как массовые силы 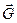имеют потенциал П, то

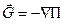(2.81)

Кроме того, пусть существует функция давления

(2.82)

Течения, в которых плотность зависит только от давления, на­зываются баротропными. Градиент функции 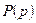, равный

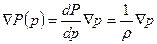
может рассматриваться как вектор объемного действия поверх­ностных сил, а сама функция 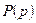как потенциал объемно­го действия поверхностных сил.

Таким образом, (2.80) дает

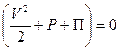
Сумму, стоящую в скобках, называют трехчленом Бернулли и обозначают как В: .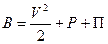

Итак, 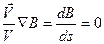, где означает производную, взятую вдоль линии тока. Отсюда следует, что B=const или

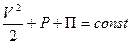(2.83)

Напомним, что это соотношение справедливо вдоль линии тока. При переходе от одной линии тока к другой константа, в принципе, может изменяться. Равенство (2.83) будет справедливо по всей области течения, если 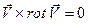, что возможно при 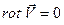или при .

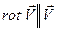Равенство (2.83) носит название интеграла Бернулли. Соотно­шение (2.83) часто называют также теоремой (уравнением) Бернулли.

В гидромеханике (и особенно в гидравлике) наиболее распрост­раненным является случай интеграла Бернулли для несжимаемой жидкости. Положим ρ=const. Тогда 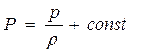. Будем считать, что жидкость находится только под действием сил тяжести, т. е. 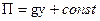, где y – ось, направленная вертикально вверх. Та­ким образом, теорема Бернулли принимает следующую форму:

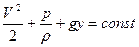(2.84)

Если поделить все члены на ускорение силы тяжести g и обо­значить константу через Н*, то можно записать

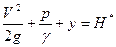, (2.85)

где 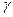– удельный вес; Н* – гидравлическая высота,

и дать теореме Бернулли классическую формулировку:

при стационарном движении тяжелой идеальной несжимаемой жидкости гидравлическая высота Н*, равная сумме скоростной 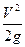, пьезометрической 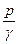и нивелирной у высот, сохраняет посто­янное значение вдоль любой линии тока (или вихревой линии).

В пренебрежении силами тяжести теореме Бернулли можно при­дать более простой вид:

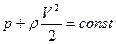(2.86)

Первый член левой части называют пьезометрическим напором или статическим давлением, второй – скоростным напором или ди­намическим давлением. Правая часть представляет собой полный напор или давление торможения.

Рассмотрим теперь адиабатическое течение воды в рамках невесомой идеальной жидкости. В соответствии с уравнением Тэйта будем иметь

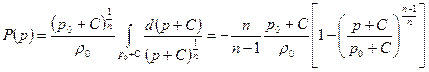
Таким образом, теорема Бернулли для сжимаемой воды будет выглядеть так:

(2.87)

Предположим, что параметры 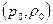жидкость приобретает в точке, где скорость обращается в нуль. Если в действительности такая точка отсутствует, то можно представить себе воображаемое движение идеальной сжимаемой жидкости, адиабатически её за­тормаживающее. Величины 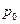и в этом случае называются соответственно давлением и плотностью торможения. При сделанном предположении уравнение (2.87) примет вид

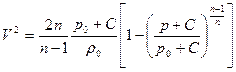(2.88)