Гидродинамические силы, и моменты, действующие на тело вращения.
В соответствии с формулами (4.15) и (4.19) получим:
 (4.20)
(4.20)
 (4.21)
(4.21)
Обратим внимание, что ранее сделанное утверждение λ26=-λ35 непосредственно следует из условия Mх=0.
Ограничим движение твёрдого тела условиями 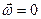 и
и 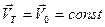 . Тогда
. Тогда 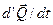 =0 и
=0 и 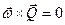 . Тогда из (4.15) и (4.19) следует
. Тогда из (4.15) и (4.19) следует
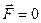 (4.22)
(4.22)
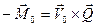 (4.23)
(4.23)
(4.22) устанавливает, что при равномерном чисто поступательном движении твёрдого тела в безграничной идеальной жидкости суммарная сила воздействия жидкости на тело равна нулю. Этот результат известен как парадокс Даламбера – Эйлера.
В этих же условиях суммарный гидродинамический момент не равен нулю. Этот момент часто называют моментом Мунка. Его существование объясняется наличием пары сил, возникающих в носовой и кормовой оконечностях тела. Эти силы равны по значению, но противоположны по направлению, что и даёт нулевую суммарную силу.
Пример. Рассмотрим равномерное чисто поступательное движение тела вращения со скоростью 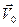 под углом атаки α в вертикальной плоскости. Компоненты скорости в связанной системе координат равны:
под углом атаки α в вертикальной плоскости. Компоненты скорости в связанной системе координат равны:
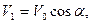
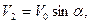
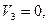
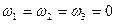
По формулам (4.20) и (4.21) находим:
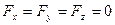
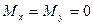
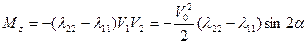 (4.24)
(4.24)
Как видим, момент действует в вертикальной плоскости и направлен по часовой стрелке, т.е. момент является опрокидывающим (или калибрирующим). Момент Mz обращается в нуль при двух значениях угла атаки: α=0º и α=90º. Обратим внимание на то, что в первом случае движение при отклонении угла атаки от положения равновесия будет приводить к появлению момента того же знака. Следовательно, движение будет статически неустойчивым. Во втором случае возникает противоположная ситуация. При отклонении угла атаки от равновесного значения α=90º создаётся момент противоположного знака, что должно приводить к уменьшению отклонения. Иными словами, во втором случае существует статически устойчивое движение. Из этого следует практический вывод, что тело вращения без оперения жидкость будет разворачивать по часовой стрелке до тех пор, пока оно не установится поперёк потока.
Множитель (λ22 - λ11 ) отражает пространственность обтекания тела, т.е. эффект взаимодействия течения в смежных слоях по потоку.
Рассмотрим теперь силовое взаимодействие твёрдого тела с идеальной жидкостью при его равномерном движении по окружности.
Подчиним движение твёрдого тела условиям:
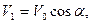
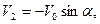
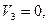
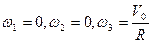
Как видим, центр масс тела описывает горизонтальную окружность радиуса R со скоростью Vo. Оси Ox и Oy тела горизонтальны и ось Ox составляет с направлением движения постоянный угол α. Ограничимся рассмотрением тела вращения. На основании (4.20)и (4.21)получим
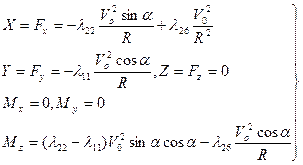 (4.25)
(4.25)
Вычислим составляющие полной гидродинамической силы F в скоростной системе координат:
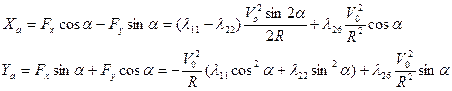
 2014-02-02
2014-02-02 1146
1146
