Теория тонкого тела (гипотеза плоских сечений)

Пусть L – характерный линейный размер в продольном направлении, a D – в поперечном. Тогда для удлиненного тела характерно неравенство

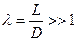
Иногда рассматривают обратную величину и тогда справед­лива оценка

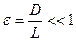
Поскольку характеризует «тонкость» тела, теорию обтекания таких тел часто называют теорией тонкого тела, понимая под тон­кими телами и плоские контуры (профили), и пространственные формы (корпуса).

Дополнительно считается, что поверх­ность удлиненных тел должна быть достаточно гладкой - не иметь изломов. Можно заключить, что при продольном движении удли­ненное тело будет мало возмущать жидкость, так что 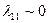. При поперечном обтекании влияние смежных слоев жидкости друг на друга будет пренебрежимо мало. Поэтому течение жидкости в каж­дом поперечном сечении, перпендикулярном продольной оси, мож­но рассматривать независимо от течения в других сечениях. Совер­шенно ясно, что течение жидкости в каждом сечении можно рас­сматривать как плоское, соответствующее обтеканию плоского кон­тура. Вот почему теорию тонкого тела отождествляют с гипотезой плоских сечений.

На практике чаще всего встречается круговое поперечное сечение корпуса. Присоединенные массы сече­ния в этом случае выражаются наиболее просто:

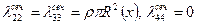
Здесь R(x) —текущий радиус поперечного сечения корпуса.

На основании теории тонкого тела присоединенные массы кор­пуса, представляющего собой тело вращения, можно представить так:

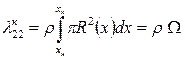(4.41)

где 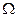– объем корпуса,

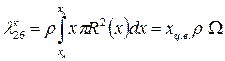(4.42)

где 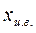– координата центра водоизмещения,

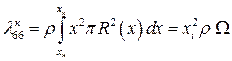(4.43)

где 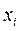– радиус корпуса инерции.

При крестообразном оперении с планами равной длины коэф­фициент присоединенной массы сечения 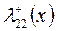определяется фор­мулой (4.37), следовательно,

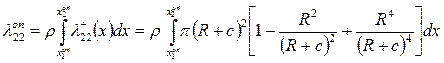(4.44)

где 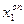, 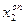– передняя и задняя координаты оперения.

Аналогично определяются и другие инерционные характеристи­ки оперения:

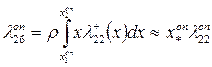(4.45)

где 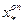– координата центра площади оперения,

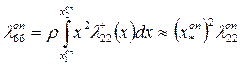(4.46)

Присоединённый момент инерции, характеризующий вращение сечения корпуса с горизонтальным оперением, равен

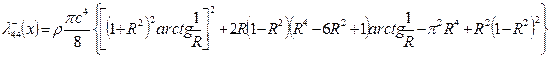(4.47)

Эта же формула дает удовлетворительные результаты и для крестообразного оперения. Таким образом, приближенно можно записать

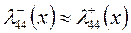
и далее

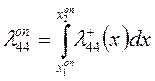(4.48)

Хвостовое оперение располагается обычно на сужающейся части корпуса, и если размах оперения незначительно превышает макси­мальный диаметр конфигурации или меньше его, то величин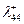а мала.

Интегралы, входящие в расчетные формулы, легко вычисляются аналитически или численно.

Аналогичным образом можно выразить присоединенные массы удлиненного корпуса с произвольным поперечным сечением и хво­стовым оперением различных очертаний. Для этого нужно, прежде всего, уметь определять присоединенные массы произвольного пло­ского контура.

При вычислении суммарных характеристик 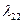, , 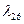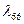необхо­димо помнить, что участок корпуса, на котором расположено опере­ние, нужно учитывать лишь один раз.