ПРИСОЕДИНЕННЫЕ МАССЫ ТЕЛ ПРОСТЕЙШЕЙ ФОРМЫ.
Простейшие задачи о течении идеальной жидкости эффективно решаются с помощью методов теории функции комплексного переменного.
Запишем единичный комплексный потенциал течения в физической плоскости z=x + iy в традиционной форме:
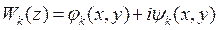 (4.26)
(4.26)
где 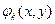 и
и 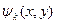 – соответственно потенциал скорости и функция тока для рассматриваемого движения,
– соответственно потенциал скорости и функция тока для рассматриваемого движения, 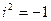 , k= 1,2,6. Циркуляционное движение отсутствует. Оси координат (x,y) совпадают с направлением осей эллипса.
, k= 1,2,6. Циркуляционное движение отсутствует. Оси координат (x,y) совпадают с направлением осей эллипса.
Для нахождения выражений воспользуемся граничными условиями:
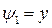 (4.27)
(4.27)
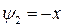 (4.28)
(4.28)
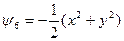 (4.29)
(4.29)
Отобразим внешность эллипса на внешность круга единичного радиуса с помощью преобразования Жуковского, затем построим комплексный потенциал и на основании перечисленных граничных условий определим 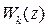 .
.
Таким образом, вычисляются присоединенные массы эллипса:
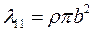 (4.30)
(4.30)
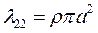 (4.31)
(4.31)
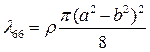 (4.32)
(4.32)
Так как контур обладает двумя осями симметрии, а начало расположено в центре фигуры, то
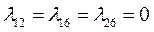 (4.33)
(4.33)
Пример. Рассмотрим произвольное движение круга радиуса R. В этом случае a=b=R. Отличным от нуля будет только одно значение присоединенной массы:
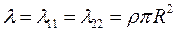 (4.34)
(4.34)
Пример. Произвольное движение тонкого эллипса, который можно определить как пластинку. Положим b=0 и a=l, l – полуширина пластины. Тогда
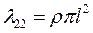 (4.35)
(4.35)

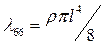 (4.36)
(4.36)
Пример. Укажем присоединенные массы круга радиуса R с крестообразными ребрами, имеющими полуразмах с, тогда:
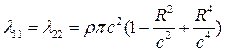 (4.37)
(4.37)
Присоединенная масса сферы равна половине массы воды, вытесненной сферой:
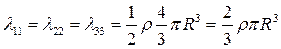 (4.38)
(4.38)
Для диска, центральная ось симметрии которого расположена вдоль оси x, найдено:
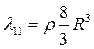 ,
,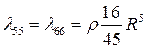 ,
,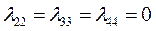 (4.39)
(4.39)
Инерционные характеристики эллипсоидов вращения принято выражать через безразмерные коэффициенты.
У сплюснутых вдоль оси x эллипсоидов (сфероидов) целесообразно присоединение массы относить к соответствующим присоединенным массам диска:
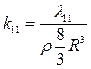 ,
, ,
,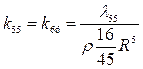
У эллипсов, вытянутых вдоль оси x, безразмерные коэффициенты присоединенных масс таковы:
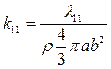 ,
,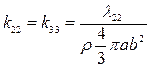 ,
,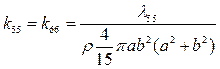 ,
,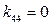
 2014-02-02
2014-02-02 1347
1347








