На основании второго закона Ньютона сила выражается через производную по времени от количества движения, а момент - через производную от момента количества движения. Следовательно, рассматривая приведённую в движение жидкость как некоторое фиктивное жидкое тело можно определить суммарную гидродинамическую силу и гидродинамический момент, действующие на это тело. С другой стороны, по третьему закону Ньютона действие равно противодействию. Таким образом, на твёрдое тело, движущееся в жидкости, будут в общем случае действовать гидродинамическая сила 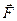 и гидродинамический момент
и гидродинамический момент 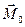
Если 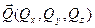 – вектор количества движения «жидкого тела», то компоненты этого вектора выражаются через производные кинетической энергии по соответствующим компонентам скоростей:
– вектор количества движения «жидкого тела», то компоненты этого вектора выражаются через производные кинетической энергии по соответствующим компонентам скоростей:
 =
=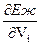 , где i =1,2,3 (4.12)
, где i =1,2,3 (4.12)
Аналогично пусть 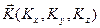 – вектор момента количества движения.
– вектор момента количества движения.
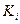 =
= 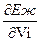 , где i =4,5,6 (4.13)
, где i =4,5,6 (4.13)
Перейдём к определению сил и моментов. В инерциальной системе координат:
-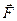 =
=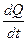 (4.14)
(4.14)
Однако векторы 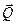 и
и 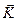 вычисляясь в неинерциальной системе координат. Поэтому в формуле (4.14) по времени нужно дифференцировать как компоненты вектора
вычисляясь в неинерциальной системе координат. Поэтому в формуле (4.14) по времени нужно дифференцировать как компоненты вектора 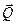 ,так и единичные векторы осей координат. Это даёт:
,так и единичные векторы осей координат. Это даёт:
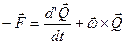 , (4.15)
, (4.15)
где штрих означает дифференцирование в подвижной системе координат при неизменном положении осей в пространстве.
Гидродинамический момент в инерциальной системе координат относительно неподвижной в пространстве точки Og равен:
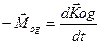 , (4.16)
, (4.16)
где 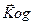 - момент количества движения относительно неподвижной точки Og.
- момент количества движения относительно неподвижной точки Og.
Введём в рассмотрение подвижную точку O,совпадающую с началом связанной системы координат. Пусть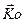 – вектор кинетического момента относительно этой точки, а
– вектор кинетического момента относительно этой точки, а 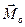 – гидродинамический момент относительно этой же точки. Тогда справедливы следующие равенства:
– гидродинамический момент относительно этой же точки. Тогда справедливы следующие равенства:
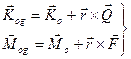 (4.17)
(4.17)
Это даёт возможность получить выражение для гидродинамического момента 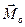 в связанной системе координат. Из (4.16) и (4.17):
в связанной системе координат. Из (4.16) и (4.17):
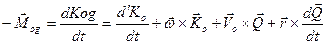 (4.18)
(4.18)
С учётом (4.17) и (4.18) окончательно находим:
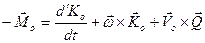 ( 4.19)
( 4.19)
 2014-02-02
2014-02-02 1435
1435








