ДЕМПФИРУЮЩИЕ ГИДРОДИНАМИЧЕСКИЕ СИЛЫ И МОМЕНТЫ
В случае управляемого движения тело совершает в жидкости различные эволюции, а потому скорость каждой точки его поверхности складываётся из поступательной скорости полюса и вращательной скорости относительно этого полюса. Наличие во внешней среде возмущений различного рода вызывает необходимость постоянной работы рулевых органов, что также способствует возникновению вращательных движений. Вращательное движение изменяет характер обтекания тела и ведет к появлению дополнительных сил и моментов. В общем, можно сказать, что при вращении тела возникают такие гидродинамические силы и моменты, которые препятствуют вращению, почему они и называются демпфирующими. Рассмотрим природу их возникновения и дадим количественную оценку этим силам и моментам.
Рассмотрим движение удлиненного тела в вертикальной плоскости ОХУ. Начало координат размещается в полюсе. Поступательная скорость равна 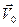 , угловая
, угловая 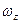 .
.
Оценим сначала демпфирующие свойства изолированного корпуса. Как следует из рассмотрения формул сил и моментов инерционной природы, действующих на тело вращения (4.27), (4.28), в условиях 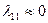 (сильно удлиненное тело вращения) приближенно можно считать
(сильно удлиненное тело вращения) приближенно можно считать 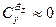 . Если
. Если 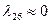 , то и
, то и 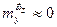 . Таким образом при вращательном движении удлиненного корпуса относительно центра водоизмещения вращательные производные сил и моментов инерционной природы приближенно равны, нулю. Отсюда следует, что демпфирующие гидродинамические силы и моменты имеют чисто вязкостную природу.
. Таким образом при вращательном движении удлиненного корпуса относительно центра водоизмещения вращательные производные сил и моментов инерционной природы приближенно равны, нулю. Отсюда следует, что демпфирующие гидродинамические силы и моменты имеют чисто вязкостную природу.
Местный угол атаки на продольной оси, обусловленны вращением, равен
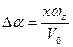 (6.33)
(6.33)
На основании гипотезы квазистационарности можно записать
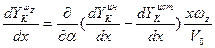 (6.34)
(6.34)
где 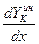 - погонная нагрузка инерционной природы;
- погонная нагрузка инерционной природы; 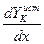 - реальная (истинная) погонная нагрузка;
- реальная (истинная) погонная нагрузка; 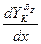 - демпфирующая погонная нагрузка вязкостной природы.
- демпфирующая погонная нагрузка вязкостной природы.
Интегрирование дает суммарную демпфирующую силу:
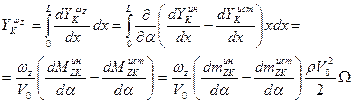
Первое слагаемое в скобках представляет собой момент Мунка для стационарного движения тела вращения под углом атаки. Второе слагаемое можно вычислить по формуле предыдущего параграфа. Однако для приближенных оценок формулы можно упростить, ограничившись рассмотрением больших удлинений и малых углов атаки, т. е. оставаясь в рамках гипотезы плоских сечений. В этом случае инерционная составляющая равна (6.32):
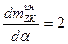
Экспериментами установлено, что реальная величина на 25% ниже указанной, т. е.
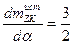
Таким образом,
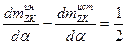
и
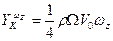 (6.35)
(6.35)
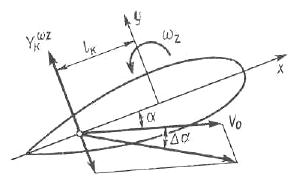 Определим теперь координату приложения демпфирующей силы lК (рис. 6.9). В точке приложения демпфирующей силы угол атаки возрастет на величину
Определим теперь координату приложения демпфирующей силы lК (рис. 6.9). В точке приложения демпфирующей силы угол атаки возрастет на величину 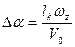 . Поэтому нормальная сила будет равна
. Поэтому нормальная сила будет равна
Рис. 6.9 Модель
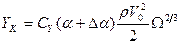 (6.36)
(6.36)
Разложим 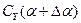 в ряд Тейлора
в ряд Тейлора
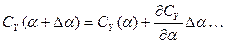
и представим нормальную силу в виде двух слагаемых
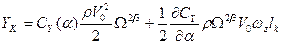
Первое слагаемое представляет обычную позиционную нормальную силу, второе - демпфирующую. Таким образом,
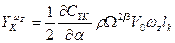 (6.37)
(6.37)
или
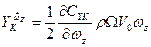 (6.38)
(6.38)
где 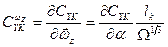 вращательная производная нормальной силы корпуса. Сопоставляя формулы (6.35) и (6.38),
вращательная производная нормальной силы корпуса. Сопоставляя формулы (6.35) и (6.38),
найдем
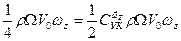
откуда следует
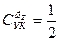 (6.39)
(6.39)
и далее
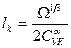 (6.40)
(6.40)
Демпфирующий момент корпуса равен произведению силы на плечо:
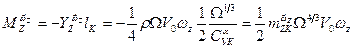 (6.41)
(6.41)
где
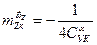 (6.42)
(6.42)
Демпфирующие свойства оперения определим аналогичным путем. Пусть расстояние от начала координат до центра площади горизонтального оперения равно lг.о. Поскольку продольный размер (хорда) оперения много меньше lг.о, можно пренебречь изменением угла атаки в пределах оперения и вычислить лишь его изменение в центре площади 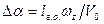 . Тогда
. Тогда
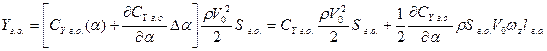
и
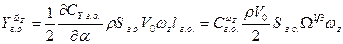 (6.43)
(6.43)
где
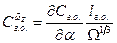 (6.44)
(6.44)
Демпфирующий момент равен
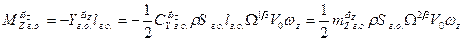
где
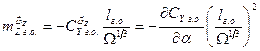
Суммируя теперь демпфирующие характеристики корпуса и горизонтального оперения, найдем
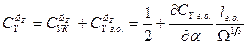 (6.45)
(6.45)
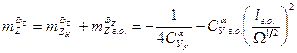 (6.46)
(6.46)
Нетрудно заметить, что 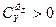 , а
, а 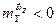 .
.
 2014-02-02
2014-02-02 1458
1458








