Картина течения в физической плоскости z изображена на рис.7.12. там же последовательно показаны схемы течения в плоскостях W, W-1, ω и t. Пользуясь теоремой Кристоффеля – Шварца, отобразим область W-1 на верхнюю полуплоскость комплексного переменного t. Вся плоскость W-1 будет являться внутренней областью относительно разреза вдоль положительных значений горизонтальной оси. Поэтому в точке С внутренний угол равен 2π, в точках В и В’ внутренние углы равны π, а точка А переходит в бесконечность и из рассмотрения выпадает. Таким образом,
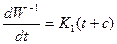
и далее
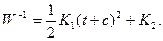 (7.13)
(7.13)
В точке С (t=-c) W-1=0 и поэтому K2=0. Отсюда
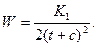 (7.14)
(7.14)
Отобразим теперь на эту верхнюю полуплоскость внутренность полуплоскость в плоскости ω. В точках В и B’ внутренние углы равны π/2, а сами точки переходяn в t= ±1. Следовательно,
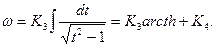 (7.15)
(7.15)
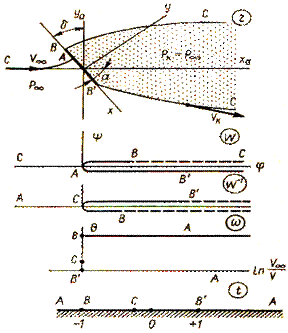
Рис. 7.12
Для нахождения констант K3 и K4 воспользуемся условием, что в точках t=±1 ω равняется соответственно, 0 и 1π. Это дает
0=iπK3+K4, -iπ=K4.
С учетом найденных констант преобразование внутренности полуполосы плоскости ω на верхнюю полуплоскость t принимает вид
ω=archt-1π (7.16)
или
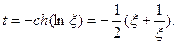 (7.17)
(7.17)
По определению, 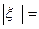 V∞/V. Поэтому на наветренной стороне пластины имеем
V∞/V. Поэтому на наветренной стороне пластины имеем
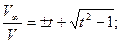
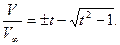 (7.18)
(7.18)
Последние соотношения позволяют определить координату с в плоскости параметрического переменного t. В самом деле, на бесконечности V/V∞=e-i(π-α), т.е. справедливо соотношение
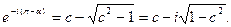
Но по формуле Эйлера
e-iα = cosα - isinα.
Поэтому
c = -cosα (7.19)
и
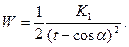 (7.20)
(7.20)
Установим связь
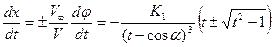 (7.21)
(7.21)
и перейдем от переменной t, которая в данном случае является действительной величиной, так как изменяется лишь вдоль действия оси на отрезках В’А и ВА, к переменной γ:
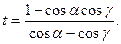 (7.22)
(7.22)
С помощью указанной подстановки получаем
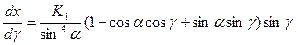
и далее
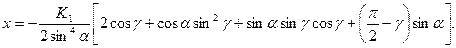
Теперь можно выразить константу K1 через заданную длину пластины l. Выберем начало координат в середине пластины. Тогда ее концы ± l /2 будут соответствовать значения углов γ=0 и γ=π. Окончательно получим
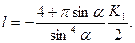 (7.23)
(7.23)
В точке разветвления потока t=±∞ и поэтому γ=α. Координата этой точки равна
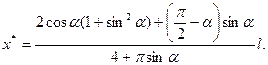 (7.24)
(7.24)
Вычислим результирующую сил давления жидкости на пластину:
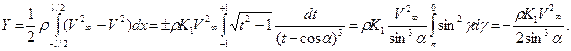 (7.25)
(7.25)
Выражая константу K1 с помощью (7.19) и подставляя найденное значение в (7.25), получим окончательное выражение для нормальной силы
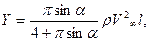 (7.26)
(7.26)
которому соответствует коэффициент нормальной силы
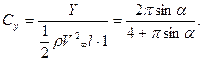 (7.27)
(7.27)
Аналогичным путем вычислим момент сил давления относительно центра пластины
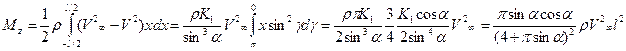 (7.28)
(7.28)
и соответствующий коэффициент момента
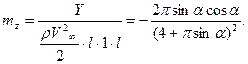 (7.29)
(7.29)
Используя выражения для нормальной силы (7.26) и продольного момента (7.23), нетрудно выразить координату центра давления:
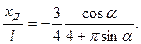 (7.30)
(7.30)
Приведенное решение получено Рэлеем.
Обратим внимание, что величина нормальной силы до α≈40° с достаточной точностью следует закону sinα. В скоростной системе координат выражения для гидродинамических коэффициентов будут равны
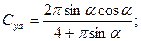 (7.31)
(7.31)
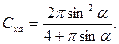 (7.32)
(7.32)
Угол α=90° отвечает случаю поперечного обтекания пластины. В этом случае
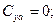
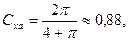 (7.33)
(7.33)
каверна имеет симметричную форму, а ее уравнение в параметрическом виде записывается следующим образом:
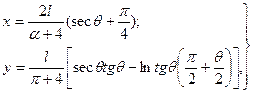 (7.34)
(7.34)
где 0≤θ≤-π/2.
 2014-02-02
2014-02-02 591
591








