Метод Н.Е.Жуковского

В плоских течениях идеальной жидкости можно ввести комплексный потенциал скорости , где 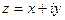. Поскольку W(z) есть аналитическая функция от комплексного переменного z, её производная не зависит от направления дифференцирования. Поэтому

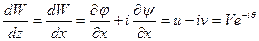, (7.10)

где 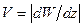, θ-полярный угол

Тот же результат получим, если продифференцируем по переменной iy. Таким образом, комплексная скорость dW/dz есть комплексно-сопряженная величина истинной скорости жидкой частицы.

Введём, следуя Н.Е. Жуковскому, функцию

. (7.11)

Согласно основному допущению классической теории развитых кавитационных течений на границах каверны скорость постоянна. Поэтому действительная часть ω на границах каверны также постоянна и определяется с помощью дополнительного соотношения 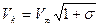. В плоскости ω границам каверны будут соответствовать вертикальные линии, отвечающие заданному значению числа кавитации.

На твердых границах известно направление скорости жидких частиц. В случае прямолинейных твердых границ в плоскости ω им будут соответствовать горизонтальные прямые θ=const. Таким образом, в плоскости ω область течения будет ограничиваться прямыми линиями и представлять собой многоугольник.

Если теперь установить взаимную связь между плоскостями W и ω, то будет решена задача о течении жидкости со свободной границей. Указанную связь выражают параметрически путем отображения плоскостей W и ω на вспомогательную плоскость t. В случае прямолинейных границ это делается с помощью преобразования Кристоффеля — Шварца.