Удар плавающего тела о жидкость

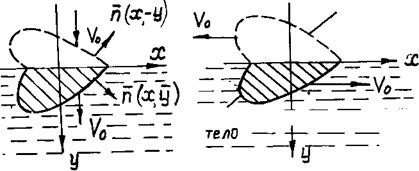
Предположим, что телу, плавающему на поверхности жидкости, в некоторый момент времени мгновенно сообщена скорость V₀ в сторону жидкости, заполняющей нижнее полупространство (смотри рисунок)

А) вертикальный удар Б) горизонтальный удар

Зеркальное отображение

Рис.8.4

Требуется определить последующее течение жидкости и ударную нагрузку на тело.

Согласно теореме Лагранжа движение жидкости будет потенциальным, так как оно возникает из состояния покоя. Следовательно, в полупространстве (Ω) должно выполняться уравнение Лапласа

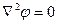(8.20)

с такими граничными условиями:

а) на поверхности тела Σ должно выполняться условие непротекания

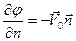(8.21)

б) на бесконечном удалении от тела жидкость покоится, и поэтому

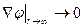(8.22)

в) на свободной поверхности давление конечно (равно атмосферному), а поэтому импульсивное давление равно нулю, следовательно, из уравнения Коши-Лагранжа

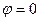(8.23)

Поясним термин «импульсивное давление»:

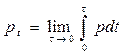
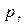может быть отличным от нуля только в случае бесконечных значений давления. В противном случае 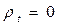. Для свободной поверхности можно записать уравнение Коши-Лагранжа и получить 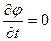и, следовательно, .

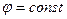Если же положить константу равной нулю, то будем иметь граничное условие (8.23)

Сформулированная задача неудобна тем, что областью определения искомой функции φ является нижнее полупространство. Однако с помощью принципа симметрии задачу определённым образом можно распространить и на верхнее полупространство, т.е. рассматривать течение в безграничной жидкости.

В случае отсутствия отрыва жидкости от твердых стенок после удара краевая задача (8.20)... (8.22) имеет единственное решение. Однако такое предположение не всегда оправдано с физиче­ской точки зрения, так как в определенных ситуациях в жидко­сти могут возникнуть области, в которых импульс давления будет отрицательным. Например, при горизонтальном ударе по телу, имеющему вертикальную плоскость симметрии, при безотрывном обтекании потенциал скоростей в точках, симметричных относи­тельно плоскости симметрии, будет иметь значения, равные по ве­личине, но противоположные по знаку. Это означает, что на тыльной стороне тела импульсы давления будут отрицательными. Чтобы устранить это несоответствие, необходимо предположить возможность отрыва потока. В зоне отрыва, очевидно, должно быть

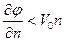и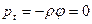

На смоченной части поверхности по-прежнему должно выполняться условие непротекания, а .