Основные методы решения задач

Существующие подходы к решению гидродинамических задач проникания тел в воду можно разделить на две большие группы:

а) точные численные методы;

б) приближенные аналитические и полуэмпирические методы.

Среди численных методов преобладают методы конечных разностей типа метода крупных частиц в сочетании с методом маркеров для слежения за движением свободных границ.

Составными элементами приближенных методов являются: метод линеаризации, теория удара метод эквивалентного тела.

Можно выделить две характерные группы очертаний окружающихся тел: тела с затупленной носовой частью и сильно заостренные тела. В первом случае при вер­тикальном входе граничное условие непротекания на твердой поверхности можно снести на горизонтальную поверхность, совпадающую с невозмущенной поверхностью воды. Но тогда задача становится эквивалентной задаче об ударе по плавающей пластине (диску в осесимметричной задаче), ширина которой зависит от глубины проникания затупленного тела. Таким образом, непрерывный процесс проникания заменяется после­довательностью ударов о поверхность покоящейся жидкости пла­стины (диска). Из динамического условия (8.4) на свободной поверхности при ударе следует

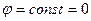. (8.14)

Если уравнение свободной поверхности y = f(x, t), то согласно кинематическому условию (8.5)

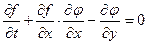. (8.15)

В условиях линеаризации получим

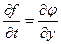(8.16)

или 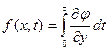(8.17)

Поскольку удар происходит за бесконечно малый промежуток времени, а скорости на свободной поверхности можно считать конечными, деформациями свободной границы в процессе удара можно пренебречь.

За конечный интервал времени погружения тела на некоторую глубину свободная поверхность примет конфигурацию, определяемую формулой (8.15). Максимальный подъем свободной поверхности определится пересечением свободной поверхности f(x, t) с контуром погружающегося тела

у = η(х), т.е. уравнением

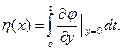(8.18)

Таким образом, истинная ширина эквивалентной пластины (радиус диска) с учетом встречного движения воды будет больше. Поправка будет зависеть от конкретной конфигурации погружаю­щегося тела и должна находиться из решения интегрального уравнения (8.18)

Рис.8.3

Указанный подход при умеренных затуплениях будет, естествен­но, давать завышенные значения гидродинамических нагрузок. Поэтому для совпадения с экспериментальными данными вводят дополнительные упрощения, зачастую недостаточно аргументированные с физической точки зрения. Логически более обоснованным представляется выбор другого эквивалентного тела в ударной за­даче, нежели пластина (диск). Прежде всего следует попытаться решить ударную задачу для реальной конфигурации погруженной части.

Если же это сделать затруднительно, можно использовать в качестве эквивалентного тела эллипс (или эллипсоид вращения), од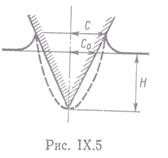на из осей которого равна глубине погружения, а другая—полуширине (радиусу) контура смачивания (рис. 8.3).

В случае проникания в воду сильно заостренного тела (например, узкого клина, тонкого конуса) линеаризацию можно осуществить относительно продольной оси и затем решать задачу методом осевого распределения особенностей (источников, стоков, диполей), зачастую с привлечением идей теории плоских сечений.

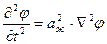(8.19)

Вход в воду сопровождается пиковыми нагрузками, что вызывают деформации и колебательные процессы в погружающихся конструкциях. Таким образом возникает проблема совместного решения уравнений гидромеханики, динамики и прочности.