Математические модели при входе тел в воду

Моделирование сжимаемости воды.

Основным критерием, ха­рактеризующим сжимаемость среды, является число Маха. В воде скорость звука велика (а_ж ~1500 м/с). Поэтому наблюдать и оценивать эффекты сжимаемости при входе в воду можно лишь в слу­чае очень больших скоростей приводнения. Это трудно реализо­вать технически. А кроме того, продолжительность эксперимента при больших скоростях входа становится чрезвычайно малой, что сильно затрудняет выполнение измерений и наблюдения за харак­тером течения. Поэтому логичным является предложение исполь­зовать в экспериментах вместо воды другую жидкую среду, ско­рость звука в которой существенно меньше скорости звука в воде, а уравнение состояния в некотором диапазоне параметров незна­чительно отличается от уравнения состояния Тэйта для воды. Ука­занным условиям удовлетворяет мелкодисперсная смесь глицерина с пузырьками газа при объемной концентрации газа, равной 1/3. В этом случае удается достичь чисел Маха порядка 0,75 при ско­ростях приводнения до 16 м/с.

Опираясь на анализ влияния различных физических факторов, на последовательные стадии погружения, можно сформулировать достаточно обоснованные математические модели течений.

С точки зрения прочности наибольшего внимания требует ста­дия проникания, поскольку именно на ней возникают максималь­ные нагрузки. Жидкость можно принять идеальной. Сжимаемость жидкости можно принимать во внимание или считать ее несжимаемой.

Для заостренных конфигураций при умеренных скоростях про­никания модель несжимаемой жидкости является обоснованной. Для затупленных конфигураций (падение диска плашмя, напри­мер) более подходящей является модель сжимаемой жидкости. В последнем случае возможен и другой подход. Можно предположить, что при приближении плоской площадки к невозмущенной свободной поверхности воды между падающим телом и водой формируется сжатая воздушная прослойка. Воздух вытесняется из за­зора. Под действием повышенного давления свободная поверхность воды деформируется и удар плоского тела происходит по криво­линейной поверхности. Воздушная прослойка, таким образом, демп­фирует первоначальный удар о воду и это происходит до тех пор, пока увлеченный вниз газовый пузырь не всплывет. С математиче­ской точки зрения учет воздушной прослойки вызывает необходи­мость рассмотрения совместного движения двух сред: жидкостной и газовой.

Между тем предварительные расчет­ные и экспериментальные анализы показывают, что весомость воды при Fr≥3...4 не оказывает заметного влияния на суммарные силы и моменты. Поэтому в математической модели жидкость на стадии проникания можно считать невесомой.

Итак, будем считать жидкость идеальной, несжимаемой, неве­сомой. Поскольку течение возникает из состояния покоя, оно будет потенциальным. Сформулируем для оговоренных условий задачу о проникании твердого тела.

Пусть свободная поверхность описывается уравнением в неявном виде

S(x,у, z, t)=0. Тогда во всем нижнем полупространстве, ограниченном свободной поверхностью S и твердой поверхностью погружающегося тела Σ, течение должно удовлетворять уравнению Лапласа:

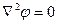(8.2)

На твёрдой поверхности погружающегося тела

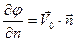(8.3)

где 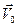— скорость точек поверхности погружающегося тела; 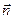— единичная нормаль к Σ, направленная внутрь жидкости. На свобод­ной поверхности должны выполняться два граничных условия:

а) динамическое условие требует равенства давления на поверх­ности жидкости атмосферному давлению p_атм. Из интеграла Коши — Лагранжа тогда получаем на S:

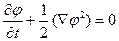(8.4)

Здесь опущены силы тяжести и не учтены силы поверхностно­го натяжения;

б) кинематическое условие устанавливает требование

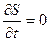(8.5)

На бесконечно большом удалении от погружающегося тела жидкость предполагается неподвижной, т.е.

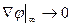(8.6)

И наконец, необходимо установить начальные условия. В на­чальный момент времени при t=0 обычно задается нулевое поле скоростей, горизонтальная свободная поверхность и начальная ско­рость приводнения 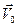по величине и направлению. В некоторых случаях начальные условия могут быть более сложными: может быть задано начальное поле скоростей, криволинейная форма сво­бодной поверхности (например, в случае падения тел на возмущенную поверхность).

Суммарную силу сопротивления жидкости определяют путем интегрирования давления по смоченной поверхности погружающегося тела:

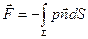(8.7)

Если жидкость рассматривается как сжимаемая среда, то при­меняется уравнение состояния воды Тэйта, а формулировка задачи может быть выполнена либо с использованием понятия потенциала скорости, либо непосредственно в физических переменных в форме законов сохранения. Остановимся на последнем подходе. Система уравнений, описывающих двухмерную задачу (плоскую или осесимметричную), будет выглядеть так:

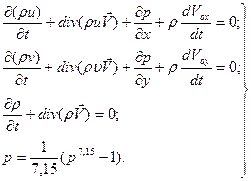(8.8)

Граничные условия:

а) на свободной поверхности

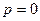(8.9)

б) на поверхности проникающего тела

(8.10)

где r=η(у) — уравнение образующей погружающегося тела в связанной системе координат.

Сила сопротивления вертикально погружающегося тела вращения равна

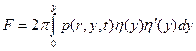(8.11)

Прямолинейное вертикальное движение тела массы т может быть записано в неподвижной (инерциальной) системе координат:

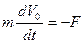(8.12)

с начальными условиями:

при t = 0 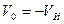(8.13 )