2014-02-02
707
В отличие от удара о воду, в процессе которого в силу его кратковременности свободные границы не изменяют своей конфигурации, при проникании свободная поверхность деформируется и этот фактор существенным образом сказывается на общей картине течения и на характеристиках силового взаимодействия погружающегося тела с жидкостью.
Примем за основу приближенную «ударную» теорию погружения. В качестве эквивалентного тела выберем эллипсоид вращения.
Присоединенные массы μ22 при центральном вертикальном ударе вытянутого (λ>1) и сжатого эллипсоида (λ<1) о воду приведены в предыдущем параграфе. Размеры эквивалентного эллипсоида необходимо скорректировать с учетом встречного движения свободной поверхности воды. Следуя Вагнеру, кинематику свободной поверхности будем рассчитывать, исходя из полученного решения задачи об ударе. Таким образом, чтобы найти горизонтальную полуось эллипсоида вращения с учетом встречного движения воды, нужно решить интегральное уравнение (8.18). Обозначим эту полуось через «с» (рис. 8.6), а отношение с/со через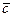 
.
|
|
|
|
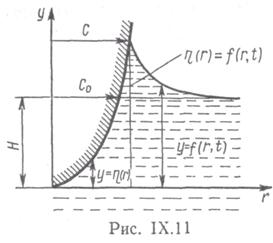
Введем новую функцию
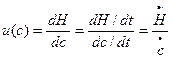
и перепишем кинематическое условие на контуре смачивания (8.18) в другом виде:
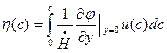(8.40)
Искомой функцией в данном уравнении является η(с). Конкретный вид уравнение приобретает при явном задании зависимосте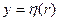й 
и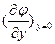 
В случае эллипсоида вращения: при 0 <λ<1 (сжатый эллипсоид)
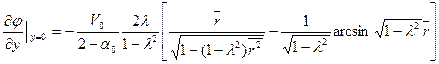(8.41)
при λ> 1 (вытянутый эллипсоид)
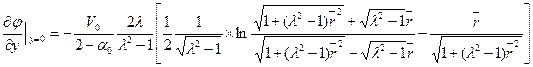(8.42)
где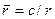
.
В случае диска (λ=0)
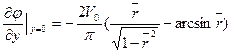(8.43)
в случае сферы (λ= 1)
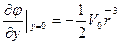(8.44)
Аналитические решения рассматриваемого уравнения удается получить для простейших геометрических очертаний (например, конуса, сферы, параболоида) и при дополнительных ограничениях на эквивалентное тело, принимая в качестве такового, например, диск или сферу. В случае геометрии погружающегося тела, близкой к эллипсоиду вращения, уравнение (8.40) необходимо решать численным путем.
