2014-02-02
1223
Принцип компенсации основан на теореме о компенсации, которая гласит: в любой электрической цепи без изменения токов в ее ветвях сопротивление в произвольной ветви можно заменить источником с ЭДС, численно равной падению напряжения на этом сопротивлении и действующей навстречу току в этой ветви.
Для доказательства теоремы выделим из схемы произвольную ветвь с сопротивлением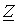 
, по которой протекает ток 
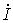, а всю остальную часть схемы условно обозначим некоторым активным двухполюсником А (см. рис. 6,а).
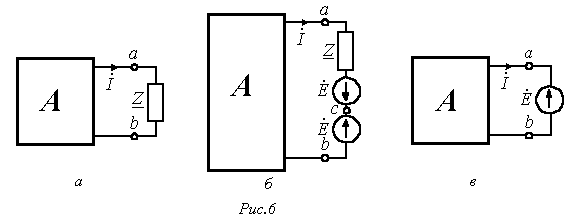
При включении в ветвь с 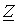двух одинаковых и действующих навстречу друг другу источников ЭДС с 
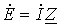(рис. 6,б) режим работы цепи не изменится. Для этой цепи
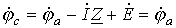 . | (12) |
Равенство (12) позволяет гальванически соединить точки а и c, то есть перейти к цепи на рис. 6,в. Таким образом, теорема доказана.
В заключение следует отметить, что аналогично для упрощения расчетов любую ветвь с известным током 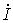можно заменить источником тока 
.
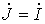Лекция N 7
