Рис. 1.1
В прямоугольниках на рис. 1.1 указана длительность технологических операции при изготовлении одного изделия каждого вида. Так как эти технологические операции используются фирмой и для других производственных целей, фонд рабочего времени, в течение которого операции 1, 2 и 3 могут быть применены для производства рассматриваемых изделий, ограничен следующими предельными значениями (в сутки):
для первой операции — 430 мин,
для второй операции — 460 мин,
для третьей операции — 420 мин.
Изучение рынка сбыта показало, что ожидаемая прибыль от продажи одного изделия видов 1, 2 и 3 составляет 3, 2 и 5 руб. соответственно.
Каков наиболее выгодный суточный объем производства каждого вида продукции?
Словесная формулировка задачи
Для фирмы требуется определить суточные объемы производства изделий каждого вида (переменные модели), при которых максимизируется общая прибыль (целевая функция), при условии, что время использования каждой технологической операции в течение суток не превышает соответствующего предельного значения (ограничения).
Математическая формулировка
Построение математической модели следует начинать с идентификации переменных. После этого определяются целевая функция и ограничения через соответствующие переменные. Главным моментом построения модели является идентификация переменных.
Пусть
x1 — количество изделий вида 1,
x2 — количество изделий вида 2,
x3 — количество изделий вида 3.
Или в более общей форме:
xj — количество изделий j -го вида, где j =1, 2 и 3.
При использовании этих обозначений математическая формулировка задачи принимает вид:
максимизировать F = 3х1 + 2х2 + 5x3 (величина прибыли за сутки)
при ограничениях
|
 для операции 1 1 x1 + 2 x2 + 1 x3 £ 430
для операции 1 1 x1 + 2 x2 + 1 x3 £ 430 для операции 2 3 x1 + 0 x2 + 2 x3 £ 460
для операции 3 1 x1 + 4 x2 + 0 x3 £ 420
" х ³ 0, (условие неотрицательности переменных).
Главным отличием этой модели является наличие более двух переменных. В этом случае возможность графического решения задачи становится по крайней мере проблематичной. Для решения задач ЛП с большим числом переменных существует алгебраический метод (симплекс метод).
Пример 1.6. (Задача составления кормовой смеси, или задача о диете.) Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный расход корма для цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 кг.
Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов. Обычно перечень ингредиентов достаточно широк, но для того, чтобы проиллюстрировать процесс построения модели, ограничимся только тремя ингредиентами: известняком, зерном и соевыми бобами. Требования к питательности рациона сформулируем также в упрощенном виде, учитывая только три вида питательных веществ: кальций, белок и клетчатку. В табл. 1.2 приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Таблица 1.2
| Ингредиент | Содержание питательных веществ, кг/(кг ингредиента) | Стоимость руб. /кг | |||
| Кальций | Белок | Клетчатка | |||
| Известняк | 0,38 | - | - | 0,04 | |
| Зерно | 0,001 | 0,09 | 0,02 | 0,15 | |
| Соевые бобы | 0,002 | 0,50 | 0,08 | 0,40 |
Заметим, что известняк не содержит ни белка, ни клетчатки.
Смесь должна содержать:
1) не менее 0,8%, но не более 1,2% кальция;
2) не менее 22% белка;
3) не более 5% клетчатки.
Словесная формулировка задачи
Для птицеводческой фермы требуется определить количество (в кг) каждого из трех ингредиентов (переменные), образующих смесь минимальной стоимости (целевая функция) при соблюдении требований к общему расходу кормовой смеси и ее питательности (ограничения).
Математическая формулировка
Введем следующие обозначения:
x1 — содержание известняка в смеси, кг;
x2 — содержание зерна в смеси, кг;
x3 — содержание соевых бобов в смеси, кг.
Так как x1, x2 и x3 представляют веса трех ингредиентов, используемых для составления смеси, общий вес смеси будет равен x1 + x2 + x3 , причем эта сумма не должна быть меньше 20000 кг.
Так как общий расход кормов равен x1 + x2 + x3 , содержание кальция должно находиться в пределах от 0,008 (x1 + x2 + x3) до 0,012 (x1 + x2 + x3). В соответствии с табл. 1.2 содержание кальция, обусловленное включением в смесь x1 кг известняка, Х2 кг зерна и Х3 кг соевых бобов, равно
0,38 x1 + 0,001 x2 + 0,002 x3 . Отсюда следует, что ограничения, связанные с содержанием кальция в кормовом рационе, можно представить в следующем виде:
1. Смесь должна содержать не менее 0,8% кальция:
0,38 x1 + 0,001 x2 + 0,002 x3 ³ 0,008(x1 + x2 + x3).
2. Смесь должна содержать не более 1,2% кальция.
0,38 x1 + 0,001 x2 + 0,002 x3 £ 0,012(x1 + x2 + x3).
Эти ограничения можно записать в более простой форме, объединив в левых частях неравенств члены, содержащие x1 , x2 и x3:
0,372 x1 - 0,007 x2 - 0,006 x3 ³ 0;
0,368 x1 - 0,011 x2 - 0,01 x3 £ 0.
Окончательная математическая формулировка задачи может быть представлена в следующем виде:
Минимизировать F = 0,04 x1 + 0,15 x2 + 0,40 x3
при ограничениях: 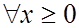
x1 + x2 + x 3 = 20000 (минимальный недельный
рацион),
|
 0,372 x1 - 0,007 x2 - 0,006 x3 ³ 0,
0,372 x1 - 0,007 x2 - 0,006 x3 ³ 0, 0,368 x1 - 0,011 x2 - 0,01 x3 £ 0.
0,220 x1 + 0,13 x2 - 0,280 x3 £ 0 (содержание белка),
0,050 x1 + 0,03 x2 - 0,030 x3 ³ 0 (содержание клетчатки).
 |
Пример 1.7.(Сменно-суточное планирование работы автобусного парка.) Исследуются возможности более рациональной организации работы городского автобусного парка с целью снижения интенсивности внутригородского движения. На начальном этапе исследования было определено минимальное количество автобусов, которым можно удовлетворить существующую потребность в пассажирских перевозках.
Сбор и обработка необходимой информации позволили сделать вывод, что минимальное количество автобусов, которым можно удовлетворить потребности в перевозках, существенно меняется в течение суток. При дальнейшем анализе было обнаружено,что требуемое количество автобусов можно считать величиной постоянной в пределах каждого из следующих друг за другом четырехчасовых интервалов (рис. 1.2). В результате проведенного исследования было решено, что с учетом необходимых затрат времени на текущий ремонт и обслуживание непрерывное исполь-зование автобусов на линии должно продолжаться только по 8 ч в сутки.
Словесная формулировка задачи
Требуется определить количество автобусов в каждой из смен (переменные), которое должно быть не меньше минимальной потребности в них (ограничения), при условии что общее количество автобусов, выходящих на линию в течение суток, будет минимальным (целевая функция).
Математическая формулировка
Как уже можно было заметить, словесные формулировки, относящиеся к определению переменных модели, не обладают требуемой однозначностью. Известна продолжительность смены — 8 ч, однако не известно, когда должна начинаться та или иная смена. Если ориентироваться на общепринятый трехсменный график работы (8:01 — 16:00; 16:01 — 24:00; 24:01 — 8:00) и обозначить количество автобусов, выходящих на линию в первую, вторую и третью смены через x1, x2,и x3 соответственно, то из рис. 1.2 можно увидеть, что x1 ³ 10, x2 ³ 12 и x3 ³ 8. Поэтому общее минимальное количество используемых автобусов будет равно x1 + x2 + x3 = 10 + 12 + 8 = 30.
Это решение приемлемо лишь в том случае, если расписание смен будет соответствовать обычному трехсменному графику работы. Однако может оказаться, что выгоднее график работы, составленный на основе оптимального выбора начала каждой из смен. Можно, например, принять такой график работы, когда начало одной смены смещено относительно начала следующей смены на 4 ч. Такой график работы с перекрывающимися сменами показан на рис. 1.3 для случая, когда смены начинаются в 0:01, 4:01, 8:01, 12:01, 16:01, 20:01, причем продолжительность смены составляет 8 ч. Теперь действительно есть возможность идентифицировать переменные, для чего целесообразнее использовать следующие обозначения:
x1 - число автобусов, выходящих на линию в 0:01,
x2 - число автобусов, выходящих на линию в 4:01,
x3 - число автобусов, выходящих на линию в 8:01,
x4 - число автобусов, выходящих на линию в 12:01,
x5 - число автобусов, выходящих на линию в 16:01,
x6 - число автобусов, выходящих на линию в 20:01.
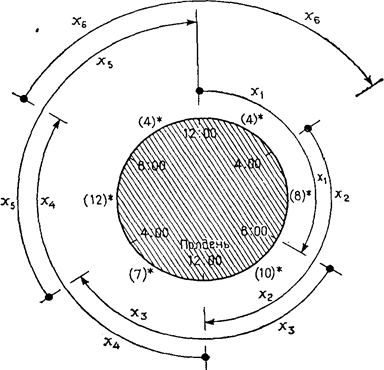
Рис. 1.3
Примечание. Знак * означает минимальную потребность в автобусах для четырехчасовых интервалов.
Соответствующая рис. 1.3 математическая модель записывается следующим образом:
Минимизировать F = x1 + x2 + x3 + x4 + x5 + x6
при ограничениях
x1 + x6 ³ 4 (с 0:01 до 4:00),
x1 + x2 ³ 8 (с 4:01 до 8:00),
x2 + x3 ³ 10 (с 8:01 до 12:00),
x3 + x4 ³ 7 (с 12:01 до 16:00),
x4 + x5 ³ 12 (с 16:01 до 20:00),
x5 + x6 ³ 4 (с 20:01 до 0:00),
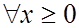
Пример 1.8. (Минимизация дисбаланса на линии сборки.)
Промышленная фирма производит изделие, представляющее собой сборку из трех различных узлов. Эти узлы изготовляются на двух заводах. Из-за различий в составе технологического оборудования производительность заводов по выпуску каждого из трех видов узлов неодинакова. В табл.1.3 содержатся исходные данные, характеризующие как производительность заводов по выпуску каждого из узлов, так и максимальный суммарный ресурс времени, которым в течение недели располагает каждый из заводов для производства этих узлов.
Таблица 1.3
| Завод | Максимальный недельный фонд времени, ч | Производительность, узел/ч | ||
| Узел 1 | Узел 2 | Узел З | ||
Идеальной является такая ситуация, когда производственные мощности обоих заводов используются таким образом, что в итоге обеспечивается выпуск одинакового количества каждого из видов узлов. Однако этого трудно добиться из-за различий в производительности заводов. Более реальная цель состоит, по-видимому, в том, чтобы максимизировать выпуск изделий, что, по существу, эквивалентно минимизации дисбаланса, возникающего вследствие некомплектности поставки по одному или двум видам узлов.
Возможный объем производства каждого из трех видов узловзависит от того, какой фонд времени выделяет каждый завод для их изготовления. Это послужит для нас исходным моментом идентификации переменных.
Словесная формулировка задачи
Требуется определить еженедельные затраты времени (в часах) на производство каждого из трех видов узлов на каждом заводе (переменные), не превышающие в сумме временные ресурсы каждого завода (ограничения) и обеспечивающие максимальный выпуск изделий (целевая функция).
Математическая формулировка
Пусть xij — недельный фонд времени (в часах), выделяемый на заводе i для производства узла j. Тогда объемы производствакаждого из трех комплектующих узлов будут равны:
узел 1: 8 x11 + 6 x21,
узел 2: 5 x12 + 12 x22,
узел 3: 10 x13 + 4 x23.
Так как в конечной сборке каждый из комплектующих узлов представлен в одном экземпляре, количество конечных изделий должно быть равно количеству комплектующих узлов, объем производств которых минимален. Если, например, объем производства двухзаводов составляет 100, 112 и 108 соответствующих узлов, то количество конечных изделий будет равно min [100, 112, 108]=100. Значит, количество конечных изделий можно выразить через число комплектующих узлов следующим образом:
Min [8 x11 + 6 x21, 5 x12 + 12 x22, 10 x13 + 4 x23 ].
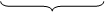

 узел 1 узел 2 узел 3
узел 1 узел 2 узел 3
Условия рассматриваемой задачи устанавливают ограничения только на фонд времени, которым располагает каждый завод. Таким образом, математическую модель можно представить в следующем виде:
Максимизировать F = min [8 x11 + 6 x21, 5 x12 + 12 x22, 10 x13 + 4 x23 ] при ограничениях
x11 + x12 + x13 £ 100 (завод 1),
x21 + x22 + x23 £ 80 (завод 2),
xij ³ 0, i = 1, 2; j = 1, 2, 3.
Эта модель не является линейной, но ее можно привести к линейной форме с помощью простого преобразования. Пусть у — количество изделий = min [8 x11 + 6 x21, 5 x12 + 12 x22, 10 x13 + 4 x23 ].
Этому выражению с математической точки зрения эквивалентна следующая формулировка: максимизировать у
при ограничениях 8 x11 + 6 x21 ³ y,
5 x12 + 12 x22 ³ y,
10 x13 + 4 x23 ³ y,
где y ³ 0 по определению. Можно убедиться в том, что максимизация у будет приводить к равенству этой переменной, наименьшей из левых частей трех введенных ограничений, а это как раз и требуется.
Таким образом, окончательно математическую модель можно записать в виде: максимизировать F = y
при ограничениях 8 x11 + 6 x21 - y ³ 0,
5 x12 + 12 x22 - y ³ 0
10 x13 + 4 x23 - y ³ 0
x11 + x12 + x13 £ 100,
x21 + x22 + x23 £ 80,
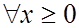 ,
,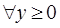 .
.
Пример 1.9. (Целевое программирование.)
Во всех предыдущих примерах ограничения представляют собой соот ношения, правые и левые части которых связаны знаками ³, £ или =. Однако при построении моделей, адекватных реальным ситуациям, иногда целесообразно отразить тот факт, что при соответствующей компенсации (штрафе) можно допустить нарушение того или иного ограничения. Это можно пояснить на следующем примере. Фирма, предпринимающая меры по организации нового производства, обычно имеет ограниченный инвестиционный фонд, но может увеличить объем капиталовложений за счет займа необходимых средств. Штраф в этом случае есть процент, под который был получен заем. Естественно, что привлечение заемных средств окажется экономически оправданным только в том случае, если новое производство будет прибыльным с учетом выплачиваемых процентов. Такой вид математического моделирования часто называют целевым программированием, так как уже сама формулировка модели ориентирована на нахождение уровня использования тех или иных ресурсов, который соответствовал бы цели, поставленной лицом, принимающим решение.
Модель целевого программирования рассмотрим на следующем простом примере. При изготовлении изделий двух видов осуществляется последовательная обработка соответствующих заготовок на двух различных станках. Каждый станок может использоваться для производства изделий по 8 ч в сутки, однако этот фонд времени можно увеличить на 4 ч за счет сверхурочных работ. Каждыйчассверхурочного времени требует дополнительных расходов в размере 5 руб. Производительность станков и прибыль в расчете на одно изделие приведены в табл. 1.4. Требуется определить объемы производства изделий каждого вида, обеспечивающие получение максимально чистой прибыли.
Таблица 1.4
| Станок | Производительность, изделие/ч | |
| Изделие 1 | Изделие 2 | |
| Удельная прибыль | 6 руб. | 4 руб. |
Словесная формулировка задачи
Требуется определить количество изделий каждого вида (переменные), которые нужно изготовить, чтобы максимизировать чистую прибыль (целевая функция), при условии, что время использования станков может быть увеличено только за счет сверхурочных работ (ограничения).
Математическая формулировка
Данная задача подобна той, которая была рассмотрена в примере 1.4. Основное отличие состоит в том, что сверхурочные работы требуют дополнительныхрасходов.
Пусть
xj — количество изделий j, j - 1, 2.
Если сверхурочные работы не допускаются, то ограничения имеют вид
x 1 /5 + x 2 /6 £ 8 (станок 1),
x 1 /4 + x 2 /8 £ 8 (станок 2).
Чтобы учесть возможность сверхурочных работ, можно видоизменить эти ограничения следующим образом:
x 1 /5 + x 2 /6 - y 1 = 8;
x 1 /4 + x 2 /8 - y 2 = 8,
где введенные переменные y 1 и y 2 не имеют ограничения в знаке, что обусловлено следующими факторами. Если переменная yi отрицательна, то имеющийся восьмичасовой фонд рабочего времени полностью не израсходован, т. е. сверхурочное время не используется. Если переменная yi положительна, восьмичасового фонда времени не хватает и используется сверхурочное время в объеме yi ч.
Вводя переменные yi, для того чтобы учесть возможность использования сверхурочного времени, мы не принимали во внимание ограничений, накладываемых на их значения. Теперь следует отразить тот факт, что продолжительность сверхурочных работ не превышает 4 ч в сутки. Кроме того, в выражении для целевой функции нужно учесть дополнительные расходы, обусловленные сверхурочными работами. Так как переменная yi положительна только в том случае, когда используется сверхурочное время, ограничения yi £ 4, i = l, 2 адекватны условиям задачи, характеризующим возможность использования сверхурочного времени. Заметим, что при yi < 0 (сверхурочные работы не выполняются) эти ограничения становятся избыточными.
Рассмотрим теперь целевую функцию. Наша цель заключается в максимизации чистой прибыли, представляющей собой общую прибыль от реализации изделий, уменьшенную на величину дополнительных расходов, связанных с выполнением сверхурочных работ. Величина общей прибыли непосредственно определяется из условий задачи как 6 x 1+4 x 2 . Следует отметить, что дополнительные расходы на сверхурочные работы учитываются только при yi > 0. Таким образом, эти дополнительные расходы удобно представить в виде:
затраты на сверхурочные работы =
=затраты/час ´ сверхурочное время (ч) =
= 5 (max {0, yi })
Заметим, что max {0, yi } = 0, если yi < 0; при этом (как и должно быть) расходы на сверхурочные работы равны нулю.
Таким образом, математическая формулировка задачи имеет вид
максимизировать F = 6 x 1 + 4 x 2 - 5 (max {0, y 1} + max {0, y 2})
при ограничениях x 1 /5 + x 2 /6 - y 1 = 8,
x 1 /4 + x 2 /8 - y 2 = 8,
y 1 £ 4,
y 2 £ 4,
x 1 , x 2 ³ 0, y 1 , y 2 не ограничены в знаке.
Для приведения модели к линейной форме используем следующую подстановку: wi = max {0, уi},
которая эквивалентна введению условий
wi ³ yi и wi ³ 0,
так как отрицательный коэффициент при wi в выражении для целевой функции влияет на нее таким образом, что в процессе оптимизации будет выбираться наименьшее из возможных неотрицательных значений, т. е. 0 или yi. Итак, модель линейного программирования для рассматриваемой задачи можно представить в следующем виде:
максимизировать F = 6 x 1 + 4 x 2 - 5(w 1 + w 2)
при ограничениях x 1 /5 + x 2 /6 - y 1 = 8,
x 1 /4 + x 2 /8 - y 2 = 8,
y 1 - w 1 £ 0,
y 2 - w 2 £ 0,
y 1 £ 4,
y 2 £ 4,
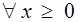 ; " w ³ 0,
; " w ³ 0,
y 1 , y 2 не ограничены в знаке.
В заключение данного раздела отметим, что характер ряда рассмотренных задач требовал введения условия целочисленности переменных для соответствующих моделей. Следует подчеркнуть, что в общем случае модель ЛП не гарантирует получения целочисленного решения, и единственный способ, который можно использовать в такой ситуации, — это округление полученных оптимальных значений переменных. Иногда такая процедура оказывается вполне приемлемой, особенно при достаточно больших значениях переменных. Основной недостаток целочисленных линейных моделей заключается в низкой эффективности соответствующих вычислительных методов.
Рассмотрим геометрическую интерпретацию задачи (1.9-1.11), для случая двух переменных.
В этом случае:
X = 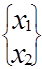 ; C =
; C =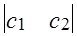 ; A =
; A =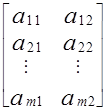 ; B =
; B = 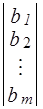
Тогда КЗЛП (1.9-1.10) может быть записана в виде:
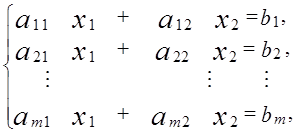 (1.12)
(1.12)

 и F = c1 x1 + c2 x2 extr.
и F = c1 x1 + c2 x2 extr.
Для геометрической интерпретации, поскольку  , берем правую верхнюю четверть плоской прямоугольной системы координат Х2OХ1, т.е. 1-й - квадрант.
, берем правую верхнюю четверть плоской прямоугольной системы координат Х2OХ1, т.е. 1-й - квадрант.
Каждое равенство из системы ограничений (1.12) дает некоторую полуплоскость в системе координат, а пересеченияm полуплоскостей образуют выпуклый многоугольник (симплекс), точки которого определяют область допустимых решений (ОДР).
Для определения точки ОДР, в которой достигается экстремум функции F, рассмотрим так называемые линии уровня, т.е. такие множества точек, на которых F имеет одно и тоже значение А.
F = c1 x1 + c2 x2 = A. (1.13)
Функция F линейна и представляет собой некоторую прямую с постоянными угловыми коэффициентами c1 и c2. При изменении 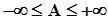 прямая уровня (1.13) функции F будет перемещаться по плоскости параллельно самой себе в направлении возрастания значений F. При таком перемещении первая точка встречи прямой с ОДР соответствует min F, а точка выхода прямой уровня из ОДР - max F (рис. 1.4).
прямая уровня (1.13) функции F будет перемещаться по плоскости параллельно самой себе в направлении возрастания значений F. При таком перемещении первая точка встречи прямой с ОДР соответствует min F, а точка выхода прямой уровня из ОДР - max F (рис. 1.4).
|
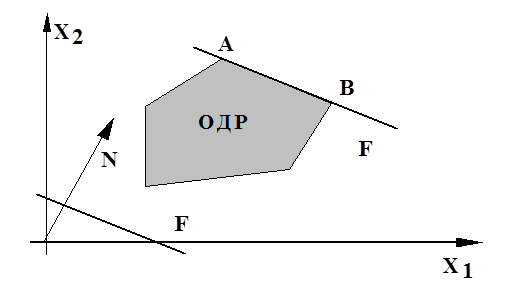
 Для получения прямой F= c1 x1 + c2 x2 = 0 построим градиент функции Fgrad N (∂F/∂x1 ,∂F/∂x2) с координатами (c1 ,c2), указывающий направление возрастания F, и через точку О проводим прямую, перпендикулярную этому вектору. Далее, построенную прямую F=0 перемещаем параллельно самой себе в направлении вектора N. На рис. 1.4 видно, что опорной по отношению к ОДР эта прямая становится в точке D. В этой точке F принимает max. Проецируя точку D, на оси ОХ1 и ОХ2 находим оптимальные значения Х1* и Х2*. Подставляя Х1* и Х2* в F находим max F, т.е. F*.
Для получения прямой F= c1 x1 + c2 x2 = 0 построим градиент функции Fgrad N (∂F/∂x1 ,∂F/∂x2) с координатами (c1 ,c2), указывающий направление возрастания F, и через точку О проводим прямую, перпендикулярную этому вектору. Далее, построенную прямую F=0 перемещаем параллельно самой себе в направлении вектора N. На рис. 1.4 видно, что опорной по отношению к ОДР эта прямая становится в точке D. В этой точке F принимает max. Проецируя точку D, на оси ОХ1 и ОХ2 находим оптимальные значения Х1* и Х2*. Подставляя Х1* и Х2* в F находим max F, т.е. F*.
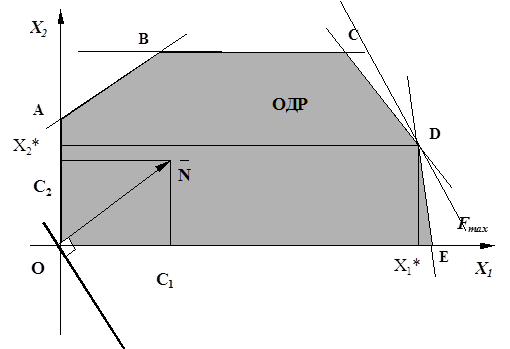
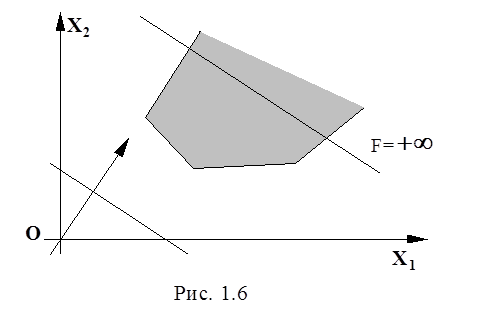
Возможны случаи, когда max F не существует (max F=+ ) рис. 1.6, либо когда оптимальное решение не единственно (min F или max F) и достигается не в одной точке, т.е. линии уровня проходят по стороне многоугольника (рис. 1.5).
) рис. 1.6, либо когда оптимальное решение не единственно (min F или max F) и достигается не в одной точке, т.е. линии уровня проходят по стороне многоугольника (рис. 1.5).
Таким образом, возможны следующие варианты:
1. Целевая функция F принимает максимальное значение в любой точке отрезка АВ, т.е. оптимальное решение не единственно. В этом случае линии уровня проходят по стороне многоугольника (рис. 1.5).
2. Целевая функция не ограничена сверху множеством допустимых значений, т.е. F max =+ (рис. 1.6).
(рис. 1.6).
3. Целевая функция не существует, поскольку система ограничений задачи несовместна.
|
Заметим, что отыскание min F для данной системы ограничений отличается от нахождения max F при тех же ограничениях лишь тем, что линия уровня c1 x1 + c2 x2 =F передвигается не в направлении 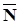 ( c1 ,c2 ), а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при определении max F, имеют место и при нахождении min F. Графическое решение задачи ЛП включает следующие этапы:
( c1 ,c2 ), а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при определении max F, имеют место и при нахождении min F. Графическое решение задачи ЛП включает следующие этапы:
1. Строят прямые, уравнения которых получают в результате замены системы неравенств на систему точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Находят ОДР.
4. Строят вектор  (c1 ,c2) с координатами (∂F/∂x1 ,∂F/∂x2).
(c1 ,c2) с координатами (∂F/∂x1 ,∂F/∂x2).
5. Строят прямую c1 x1 + c2 x2 = 0, проходящую через точку О.
6. Перемещают прямую c1 x1 + c2 x2 = 0 в сторону, совпадающую с направлением вектора  , в результате находят точку (точки), в которой (которых) целевая функция F принимает max, либо устанавливают неограниченность сверху функции на множестве планов.
, в результате находят точку (точки), в которой (которых) целевая функция F принимает max, либо устанавливают неограниченность сверху функции на множестве планов.
7. Определяют координаты точки D (X1*, X2*) и вычисляют значение целевой функции F в этой точке. Для определения координат точки D можно решить систему уравнений тех прямых, на пересечении которых лежит точка D (Рис. 1.4.)
Пример. Определить оптимальное число скорых и пассажирских поездов, при котором число перевозимых пассажиров достигает максимума для двух случаев:
а) без ограничения пропускной способности направления;
б) с ограничением по пропускной способности направления.
Исходными данными для задачи являются: наличный (рабочий) парк вагонов, схема состава (количество вагонов разных типов, обязательно включаемых в состав скорого и пассажирского поездов) и вместимость вагонов разного типа.
Пусть наличный парк вагонов, схема составов и вместимость вагонов разного типа представлены в табл. 1.5 и 1.6.
 2014-02-09
2014-02-09 2881
2881
