Алгоритм состоит из предварительного этапа и не более чем (n-2) последовательно проводимых итераций. Каждая итерация связана с эквивалентными преобразованиями матрицы, полученной в результате проведения предыдущей итерации, и с выбором максимального числа независимых нулей. Окончательным результатом итерации является увеличение числа независимых нулей на единицу.
Как только количество независимых нулей станет равным 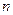 , проблема выбора оказывается решенной, а оптимальный вариант назначений определяется позициями независимых нулей в последней матрице.
, проблема выбора оказывается решенной, а оптимальный вариант назначений определяется позициями независимых нулей в последней матрице.
Предварительный этап. Разыскивают максимальный элемент в 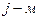 столбце и все элементы этого столбца последовательно вычитают из максимального. Эту операцию проделывают над всеми столбцами матрицы
столбце и все элементы этого столбца последовательно вычитают из максимального. Эту операцию проделывают над всеми столбцами матрицы 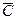 . В результате образуется матрица с неотрицательными элементами, в каждом столбце которой имеется, по крайней мере, один нуль.
. В результате образуется матрица с неотрицательными элементами, в каждом столбце которой имеется, по крайней мере, один нуль.
Далее рассматривают 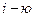 строку полученной матрицы и из каждого её элемента вычитают минимальный элемент этой строки. Эту процедуру повторяют со всеми строками. В результате получим матрицу
строку полученной матрицы и из каждого её элемента вычитают минимальный элемент этой строки. Эту процедуру повторяют со всеми строками. В результате получим матрицу 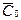 (
(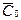 ~
~ 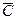 ), в каждой строке и столбце которой имеется, по крайней мере, один нуль. Описанный процесс преобразования
), в каждой строке и столбце которой имеется, по крайней мере, один нуль. Описанный процесс преобразования 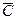 в
в 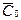 называется приведением матрицы.
называется приведением матрицы.
Находим произвольный нуль в первом столбце и отмечаем его звездочкой. Затем просматриваем второй столбец, и если в нем есть нуль, расположенный в строке, где нет нуля со звездочкой, то отмечаем его звездочкой. Аналогично просматриваем один за другим все столбцы матрицы 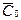 . Очевидно, что нули матрицы
. Очевидно, что нули матрицы 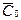 , отмеченные звездочкой, являются независимыми. На этом предварительный этап заканчивается.
, отмеченные звездочкой, являются независимыми. На этом предварительный этап заканчивается.
(k+1)-ая итерация. Допустим, что k-я итерация уже проведена и в результате получена матрица 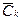 . Если в ней имеется ровно
. Если в ней имеется ровно 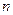 нулей со звездочкой, то процесс решения заканчивается. В противном случае переходим к (k+1) - й итерации.
нулей со звездочкой, то процесс решения заканчивается. В противном случае переходим к (k+1) - й итерации.
Каждая итерация начинается первым и заканчивается вторым этапом. Между ними может несколько раз проводиться пара этапов: третий - первый. Перед началом итерации знаком ' + ' выделяют столбцы матрицы 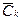 , которые содержат нули со звездочками.
, которые содержат нули со звездочками.
Первый этап. Просматривают невыделенные столбцы матрицы 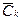 . Если среди них не окажется нулевых элементов, то переходят к третьему этапу.
. Если среди них не окажется нулевых элементов, то переходят к третьему этапу.
Если же невыделенный нуль матрицы 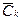 обнаружен, то возможен один из двух случаев: 1) строка, содержащая невыделенный нуль, содержит также и нуль со звездочкой; 2) эта строка не содержит нуля со звездочкой.
обнаружен, то возможен один из двух случаев: 1) строка, содержащая невыделенный нуль, содержит также и нуль со звездочкой; 2) эта строка не содержит нуля со звездочкой.
Во втором случае переходим сразу ко второму этапу, отметив этот нуль штрихом.
В первом случае этот невыделенный нуль отмечают штрихом и выделяют строку, в которой он содержится (знаком ' + ' справа от строки). Просматривают эту строку, находят нуль со звездочкой и уничтожают знак ' + ' выделения столбца, в котором содержится данный нуль.
Далее просматривают этот столбец (который уже стал невыделенным) и отыскивают в нем невыделенный нуль (или нули), в котором он находится. Этот нуль отмечают штрихом и выделяют строку, содержащую такой нуль (или нули). Затем просматривают эту строку, отыскивая в ней нуль со звездочкой.
Этот процесс за конечное число шагов заканчивается одним из следующих исходов:
1) все нули матрицы 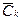 выделены, т.е. находятся в выделенных строках или столбцах. При этом переходят к третьему этапу;
выделены, т.е. находятся в выделенных строках или столбцах. При этом переходят к третьему этапу;
2) имеется такой невыделенный нуль в строке, где нет нуля со звездочкой. Тогда переходят ко второму этапу, отметив этот нуль штрихом.
Второй этап. На этом этапе строят следующую цепочку из нулей матрицы 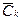 : исходный нуль со штрихом, нуль со звездочкой, расположенный в одном столбце с первым нулем со штрихом в одной строке с предшествующим нулем со звездочкой и т.д. Итак, цепочка образуется передвижением от 0 ' к 0 * по столбцу, от 0* к 0 ' по строке и т.д.
: исходный нуль со штрихом, нуль со звездочкой, расположенный в одном столбце с первым нулем со штрихом в одной строке с предшествующим нулем со звездочкой и т.д. Итак, цепочка образуется передвижением от 0 ' к 0 * по столбцу, от 0* к 0 ' по строке и т.д.
Можно доказать, что описанный алгоритм построения цепочки однозначен и конечен, при этом цепочка всегда начинается и заканчивается нулем со штрихом.
Далее над элементами цепочки, стоящими на нечетных местах (0 ' ) -, ставим звездочки, уничтожая их над четными элементами (0*). Затем уничтожаем все штрихи над элементами 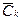 и знаки выделения ' + '. Количество независимых нулей будет увеличено на единицу. На этом (k+1) -я итерация закончена.
и знаки выделения ' + '. Количество независимых нулей будет увеличено на единицу. На этом (k+1) -я итерация закончена.
Третий этап. К этому этапу переходят после первого, если все нули матрицы 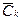 выделены, т.е. находятся на выделенных строках или столбцах. В таком случае среди невыделенных элементов матрицы
выделены, т.е. находятся на выделенных строках или столбцах. В таком случае среди невыделенных элементов матрицы 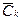 выбирают минимальный и обозначают его h (h>0). Далее вычитают h из всех элементов матрицы
выбирают минимальный и обозначают его h (h>0). Далее вычитают h из всех элементов матрицы 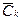 , расположенных в невыделенных строках и прибавляют ко всем элементам, расположенным в выделенных столбцах. В результате получают новую матрицу
, расположенных в невыделенных строках и прибавляют ко всем элементам, расположенным в выделенных столбцах. В результате получают новую матрицу 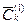 , эквивалентную
, эквивалентную 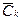 . Заметим, что при таком преобразовании, все нули со звездочкой матрицы
. Заметим, что при таком преобразовании, все нули со звездочкой матрицы 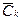 остаются нулями и в
остаются нулями и в 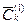 , кроме того, в ней появляются новые невыделенные нули. Поэтому переходят вновь к первому этапу. Завершив первый этап, в зависимости от его результата либо переходят ко второму этапу, либо вновь возвращаются к третьему этапу.
, кроме того, в ней появляются новые невыделенные нули. Поэтому переходят вновь к первому этапу. Завершив первый этап, в зависимости от его результата либо переходят ко второму этапу, либо вновь возвращаются к третьему этапу.
После конечного числа повторений очередной первый этап обязательно закончится переходом на второй этап. После его выполнения количество независимых нулей увеличится на единицу и (k+1) - я итерация будет закончена.
Венгерский метод является одним из интереснейших и наиболее распространенных методов решения транспортных задач.
Пример. Решить задачу выбора, которая определяется матрицей:
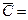 | |||||
Решение. При решении задачи используем следующие обозначения: знак выделения +, подлежащий уничтожению, обводим кружком. Цепочку во втором этапе указываем стрелками.
Предварительный этап
|
|
Первый, второй этапы
|
|
Первый, третий, первый, второй этапы
|
|
Первый, второй этапы
| + | + | + | + | |||
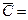 | 0* | 0 | ||||
| 1 | 0 | 0* | ||||
| 0* | ||||||
| 0* | ||||||
| 0* |
Искомые элементы матрицы соответствуют позициям независимых нулей матрицы (т. е. нулей со звездочкой).
Целевая функция 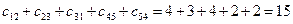
 2014-02-02
2014-02-02 1391
1391








