Графический метод
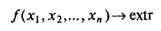


Если в задаче все ограничения или их часть либо функция цели нелинейны, то мы имеем задачу нелинейного программирования. Задачи, - в которых ограничения и функция цели линейны и предполагается целочисленность переменных, также являются нелинейными.
В задачах нелинейного программирования отсутствуют все или некоторые из свойств, характеризующих линейные задачи. Область допустимых решений в задачах линейного программирования выпукла. В задачах нелинейного программирования это свойство не сохраняется, область допустимых решений может состоять из нескольких несвязанных областей.
Таким образом, в общем случае задача нелинейного программирования является чрезвычайно трудной для решения. Если число переменных в задаче не превышает трех, то можно попытаться решить задачу графически.
Графическое решение задачи нелинейного программирования существенно отличается от такого же решения задач линейного программирования. Даже в том случае, если область допустимых решений задачи представлена системой линейных неравенств, оптимальное решение задачи может находиться в любой точке области: на границе или даже внутри области.
Рассмотрим несколько примеров графического решения таких задач.
Пример. Найти оптимальное решение задачи


Решение. Множество допустимых решений задачи — четырехугольник OEDB, представленный на рис. 1. Линии одного уровня функции цели - концентрические окружности с центром в точке А (2, 3) - точка внутри области. В этой же точке достигается минимум функции цели, равный 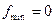 . Максимальное значение функции достигается в точке В (9, 0), где
. Максимальное значение функции достигается в точке В (9, 0), где 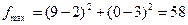 .
.

Рис. 1
Пример. Найти оптимальное решение задачи

Решение. Область допустимых решений задачи прежняя — это четырехугольник OEDB (рис. 2). Линиями одного уровня функции цели являются гиперболы, асимптотами которых служат прямые 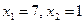 . С ростом значения
. С ростом значения 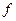 гиперболы удаляются от точки пересечения асимптот. Максимальное значение функция достигает в точке О (0, 0), где
гиперболы удаляются от точки пересечения асимптот. Максимальное значение функция достигает в точке О (0, 0), где 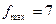 . Наименьшее значение функция достигает в гиперболе, вырождающейся в точку (7, 1), где
. Наименьшее значение функция достигает в гиперболе, вырождающейся в точку (7, 1), где 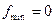 .
.
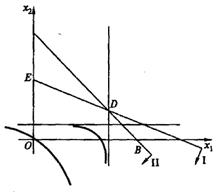
Рис. 2
Метод множителей Лагранжа
Если в задаче требуется найти экстремум функции цели при ограничениях-равенствах, т.е. имеется задача вида
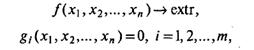
и функции 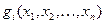 дифференцируемы, то для решения такой задачи может быть использован метод множителей Лагранжа.
дифференцируемы, то для решения такой задачи может быть использован метод множителей Лагранжа.
Сущность этого метода состоит в следующем. Вводят дополнительные переменные 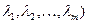 (по числу ограничений задачи) и составляют функцию, называемую функцией Лагранжа:
(по числу ограничений задачи) и составляют функцию, называемую функцией Лагранжа:


Чтобы найти оптимальное решение, определяют необходимые условия существования экстремума — равенство нулю частных производных по 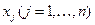 b
b 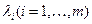 ;
;

Каждое решение системы определяет стационарную точку, в которой может достигаться экстремум функции  . Дальнейшее исследование этих точек позволяет найти решение задачи.
. Дальнейшее исследование этих точек позволяет найти решение задачи.
Пример
Методом множителей Лагранжа решить задачу:
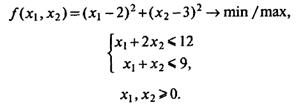
Приведем задачу к канонической форме:

Систему ограничений запишем в виде
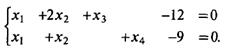
Составим функцию Лагранжа:

и приравняем ее частные производные к нулю:

Отсюда получим 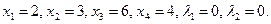 Исследуем поведение функции
Исследуем поведение функции 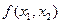 в стационарной точке (2,3). Найдем
в стационарной точке (2,3). Найдем

Следовательно, функция 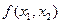 в стационарной точке (2, 3) достигает минимума, что совпадает с результатом, полученным при решении задачи графическим методом.
в стационарной точке (2, 3) достигает минимума, что совпадает с результатом, полученным при решении задачи графическим методом.
Для полного исследования поведения функции 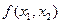 необходимо определить ее значения на границах области допустимых решений. Таких точек четыре: О (0, 0), Е (0, 6),
необходимо определить ее значения на границах области допустимых решений. Таких точек четыре: О (0, 0), Е (0, 6),
D (6, 3) и В (9, 0). Сравнивая значения функции в этих точках  и
и 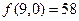 ), находим, что в точке B (9, 0) функция
), находим, что в точке B (9, 0) функция 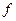 достигает наибольшего значения.
достигает наибольшего значения.
Динамическое программирование
Динамическое программирование (планирование) представляет собой математический метод для нахождения оптимальных решений многошаговых (многоэтапных) задач. Некоторые из таких задач естественным образом распадаются на отдельные шаги (этапы), но имеются задачи, в которых разбиение приходится вводить искусственно, для того чтобы их можно было решить методом динамического программирования.
Пусть на некоторый период времени Т, состоящий из т лет, планируется деятельность группы промышленных предприятий. В начале планируемого периода на развитие предприятий выделяются основные средства Q0, которые необходимо распределить между предприятиями. В процессе функционирования предприятий выделенные им средства частично расходуются. Однако каждое из этих предприятий за определенный период времени (хозяйственный год) получает прибыль, зависящую от объема вложенных средств. В начале каждого года имеющиеся средства могут перераспределяться между предприятиями. Требуется определить, сколько средств надо выделить каждому предприятию в начале каждого года, чтобы суммарный доход от всей группы предприятий за весь период времени Т был максимальным.
Процесс решения такой задачи является многошаговым. Шагом управления (планирования) здесь будет хозяйственный год. Управление процессом состоит в распределении (перераспределении) средств в начале каждого хозяйственного года.
Пусть имеется груз, состоящий из неделимых предметов различных типов, который нужно погрузить в самолет грузоподъемностью Р. Стоимость и масса каждого предмета j- готипа известны и составляют соответственно сj, и pj единиц (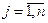 ). Требуется определить, сколько предметов каждого типа надо загрузить в самолет, чтобы суммарная стоимость груза была наибольшей, а масса не превышала грузоподъемности самолета.
). Требуется определить, сколько предметов каждого типа надо загрузить в самолет, чтобы суммарная стоимость груза была наибольшей, а масса не превышала грузоподъемности самолета.
Математически задача записывается следующим образом: найти такие целые неотрицательные значения 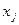 (
(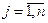 ), которые бы максимизировали функцию
), которые бы максимизировали функцию

при ограничении
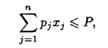
где 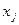 — количество груза j- готипа, позволяющее достичь
— количество груза j- готипа, позволяющее достичь 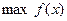 .
.
Процесс решения рассматриваемой задачи не является многоэтапным. Она относится к классу задач целочисленного линейного программирования. Однако ее можно решить методом динамического программирования. Для этого весь процесс решения потребуется разбить на этапы искусственно. На первом этапе рассматривают всевозможные варианты загрузки самолета предметами первого типа и среди них находят оптимальный. На втором этапе определяют вариант загрузки самолета предметами первого и второго типов и т. д. Процесс решения задачи продолжается до тех пор, пока не будет найден оптимальный вариант загрузки самолета предметами n типов.
 2014-02-02
2014-02-02 11843
11843
