1239
Метод динамического программирования позволяет одну задачу со многими переменными заменить рядом последовательно решаемых задач с меньшим числом переменных. Процесс решения задачи разбивается на шаги. При этом нумерация шагов, как правило, осуществляется от конца к началу.
Основным принципом, на котором базируются оптимизация многошагового процесса, а также особенности вычислительного метода динамического программирования, является принцип оптимальности Р. Беллмана.
Принцип оптимальности. Оптимальное поведение обладает тем свойством, что каковы бы ни были начальное состояние и начальное решение, последующие решения должны быть оптимальными относительно состояния, полученного в результате первоначального решения.
Принцип оптимальности имеет конструктивный характер и непосредственно указывает процедуру нахождения оптимального решения. Математически он записывается выражением вида
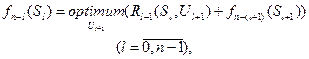(1)
где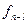 
— оптимальное значение эффекта, достигаемого за 
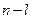шагов; п — количество шагов (этапов); 
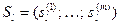— состояние системы на l-мшаге; 
— решение (управление), выбранное на l-мшаге;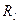 
— непосредственный эффект, достигаемый на l-мшаге.
"Optimum" в выражении (1) означает максимум или минимум в зависимости от условия задачи.
Все вычисления, дающие возможность найти оптимальное значение эффекта, достигаемого за п шагов,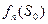 
, проводятся по формуле (1), которая носит название основного функционального уравнения Беллмана или рекуррентного соотношения. Действительно, при вычислении очередного значения функции 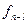используются значение функции 
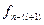, полученное на предыдущем шаге, и непосредственное значение эффекта 
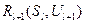, достигаемого в результате выбора решения 
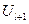при заданном состоянии системы 
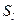. Процесс вычисления значений функции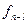 
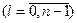осуществляется при естественном начальном условии
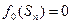, которое означает, что за пределами конечного состояния системы эффект равен нулю.
