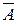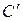Классификация СБИС программируемой логики
Глава 4.Сверхбольшие интегральные схемы
.
Глава 3. Структурный и абстрактный синтез устройств ВМ.
Таблица 24
| X | ||||||||
| Y | ||||||||
| Z | ||||||||
| S | ||||||||
| P |
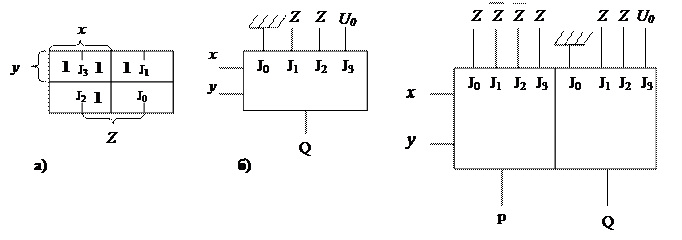
Таблица истинности (табл.24) показывает, что когда x и y равны 0, функция выхода S совпадает с z. Это означает, что на вход J0 нужно подать аргумент z. Когда x=0 и y=1 (код на шинах выборки 01), внутренние логические схемы мультиплексора срабатывают таким образом, что к этой комбинации подключается вход J1. Для этого случая таблица истинности показывает, что выход S будет равен 1 только тогда, когда z=0. Следовательно, на вход J1 (рис.6,в) нужно подать дополнение z, т.е. 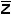 . Соответственно на вход J2 надо подать
. Соответственно на вход J2 надо подать 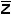 и на вход J3 - z. Это можно было определить, не прибегая к карте минимизации. Если для определения схемы подачи сигналов на входы используется карта минимизации, то требуется промежуточный этап. Карта делится на четыре двухячеечных участка, каждый из которых содержит одну ячейку для z и другую для его дополнения
и на вход J3 - z. Это можно было определить, не прибегая к карте минимизации. Если для определения схемы подачи сигналов на входы используется карта минимизации, то требуется промежуточный этап. Карта делится на четыре двухячеечных участка, каждый из которых содержит одну ячейку для z и другую для его дополнения 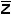 и соответствует одному из четырех входов модуля. Каждый участок карты будет содержать любую из четырех возможных комбинаций единиц и нулей (00, 01, 10, 11). Порядок расположения двоичных цифр определяет, какой сигнал должен быть получен на выходе мультиплексора и, следовательно, какой сигнал нужно подать на соответствующий вход. Если участок карты имеет код 11, на выходе всегда должен быть код 1. Для этого достаточно подать на соответствующий вход постоянное напряжение, принимаемое за уровень, соответствующий логической единице. Если участок имеет код 00, выход всегда будет 0 и на соответствующий вход нужно подать постоянный уровень для 0 (чаще всего потенциал земли). Комбинации 1 и 0 разобраны в предыдущем примере.
и соответствует одному из четырех входов модуля. Каждый участок карты будет содержать любую из четырех возможных комбинаций единиц и нулей (00, 01, 10, 11). Порядок расположения двоичных цифр определяет, какой сигнал должен быть получен на выходе мультиплексора и, следовательно, какой сигнал нужно подать на соответствующий вход. Если участок карты имеет код 11, на выходе всегда должен быть код 1. Для этого достаточно подать на соответствующий вход постоянное напряжение, принимаемое за уровень, соответствующий логической единице. Если участок имеет код 00, выход всегда будет 0 и на соответствующий вход нужно подать постоянный уровень для 0 (чаще всего потенциал земли). Комбинации 1 и 0 разобраны в предыдущем примере.
Составим логическую схему для переноса P(табл.24). На основании булева уравнения составим карту минимизации(рис.7,а). По карте минимизации составим логическую схему на половине сдвоенного четырехвходового мультиплексора (рис.7,б). В этой схеме на вход J0 подается потенциал, соответствующий сигналу 0(потенциал земли). На входы J1 и J2 подается входной сигнал z, так как функция обращается в единицу, когда z=1 и в нуль – когда z=0; на вход J3 подается сигнал, соответствующий единице, так как при любом значении z функция равна 1. Окончательно схема для одного разряда сумматора реализуется на одном сдвоенном четырехвходовом мультиплексоре (рис.8).
В целом, алгоритм определения схемы подключения сигналов ко входам мультиплексора может быть сформулирован следующим образом.
1. Составляется таблица истинности для трех переменных; определяется значение третьей переменной; берется аргумент или его отрицание или постоянные 0 или 1, которые должны быть поданы на входные шины.
2.  Составляется карта минимизации; распределяются участки карты по входам Ji.
Составляется карта минимизации; распределяются участки карты по входам Ji.
|
|
Метод использования универсальной логической схемы для функции трех переменных может быть распространен на реализацию функций четырех и более переменных. Для реализации функции четырех переменных удобнее использовать восьмивходовой мультиплексор. Покажем это на примере.
Пример. Пусть для реализации задана функция
f(ABCD)=m2+ m4+ m5+ m6+ m9+ m10+ m11+ m13.
Составим таблицу истинности (табл.25) и карты минимизации как и в предыдущем случае (рис.9,а,б). Каждый участок карты приписывается каждому из восьми входов мультиплексора. Требуемая схема подачи входных сигналов определяется при рассмотрении карты в зависимости от того, какой код в них содержится – 00, 01, 10 или 11. Для данной функции схема подключения входов имеет вид (рис.9,в):
J0 – земля, J1 – D, J2 - U0, J3 – D, J4 - 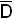 , J5 - U0, J6 -
, J5 - U0, J6 - 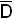 , J7 – земля.
, J7 – земля.
При реализации функции от пяти и более переменных требуется более одного уровня универсальных логических схем. В этом случае один набор логических схем вырабатывает сигналы, подаваемые на другой набор схемы. Например, для реализации функций шести переменных в общем случае требуется восемь четырехвходовых мультиплексоров (4 ИС) на первом уровне и один восьмивходовой мультиплексор на втором уровне.
Таблица 24
| A | ||||||||||||||||
| B | ||||||||||||||||
| C | ||||||||||||||||
| D | ||||||||||||||||
| f(ABCD) |
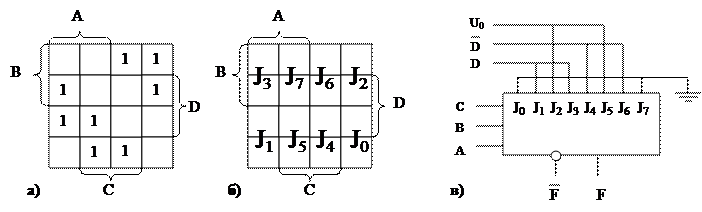
Рис.9.
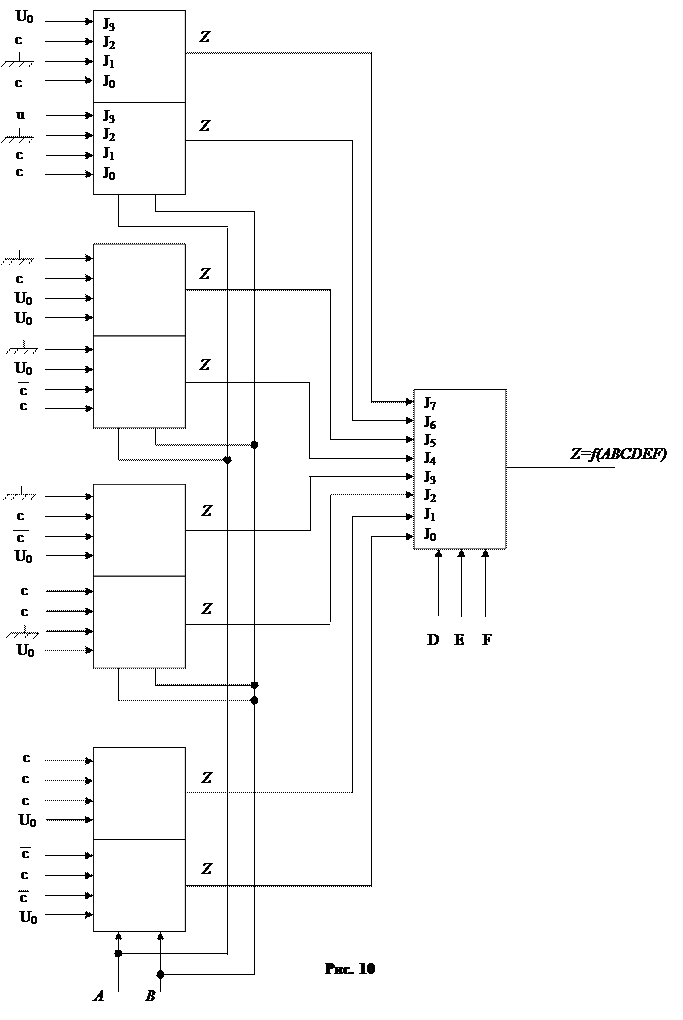
Чтобы создать схему, реализующую функцию шести переменных f(ABCDEF), переменные функции делят на две части A,B,C и D,E,F. В этом случае схемная реализация упрощается. Вместо задачи для шести переменных получаются две задачи при трех переменных, которые решаются следующим образом:
а) выделяют каждую их комбинаций D,E,F, получают функции остальных трех переменных fi(ABC), соответствующих каждой комбинации;
б) собирают все элементы функции fi(ABC), соответствующие каждому отдельному виду комбинации входных сигналов D,E,F;
в) реализуют каждую функцию переменных A,B,C как функцию трех переменных, получают выходные сигналы первого уровня;
г) подают эти входные сигналы первого уровня на восьмивходовой мультиплексор, который управляется комбинациями сигналов D,E,F, поступающими на шины выборки.
Покажем это на примере функции
f(ABCDEF)=∑0,2,4,5,6,9,10,11,12,13,14,15,17,
24,25,26,28,29,30,31,32,33,37,38,39,
43,44,45,48,51,58,59,60,63.
В таблице истинности (табл.25) покажем только те наборы, на которых функция обращается в единицу (рис.10).
В некоторых случаях схема может быть упрощена перестановкой аргументов, которые должны быть включены на первом уровне. Переменные должны располагаться так, чтобы для двух или более групп Ji их значения были бы или инверсны друг другу, или имели бы одинаковые значения. В этих случаях один и тот же элемент можно использовать несколько раз (если для некоторых Ji аргументов на первом уровне принимают одинаковые значения). Если аргументы на первом уровне для некоторых значений Ji –х принимает противоположные значения, то в этом случае можно использовать инверсию от Ji –го выхода. Заданную функцию f(ABCDEF) можно реализовать путем преобразования ее в функцию 1-го уровня f(CDB) (вместо f(ABC)) и комбинацию переменных второго уровня EFA. При такой группировке значения функции f(CDB) одинаковы для членов второго уровня J0 и J1, а член второго уровня J7 является дополнением J6. В результате такой группировки для реализации заданной функции требуется на два четырехвходовых мультиплексора меньше, чем в предыдущем случае (табл.26).


Так как последовательные устройства можно рассматривать в качестве обычных логический устройств с обратными связями, то это означает, что мультиплексор может быть использован и при реализации конечных автоматов.
Структурный синтез операционных устройств ВМ. Операционное устройство ВМ можно представить состоящим как бы из двух частей — комбинационной и памяти. На входы комбинационной части поступают сигналы с выходов элементов памяти (триггеров) Q1, …, Qm, а также сигналы, приходящие по шинам управления x1, …, xm. Назначение шин управления состоит в том, чтобы из всех микроопераций, выполняемых устройством, выбрать одну, требуемую в данный момент. Сигналы с выходов комбинационных схем подаются на входы триггеров. Функция возбуждения входного i-го триггера записывается в следующем виде:
Значения всех переменных в этом выражении определены для одного и того же момента времени t, поэтому функции возбуждения триггеров являются переключательными функциями, которым соответствуют комбинационные схемы, формирующие входные сигналы для триггеров. Следовательно, если известен тип триггера, то задача структурного синтеза устройства заключается в составлении функции возбуждения каждого триггера, функции кодирования выходов заданного устройства и минимизации. При выполнении структурного синтеза используются матрицы переходов триггеров (табл. 3.1), где для каждого типа триггера указаны значения входных сигналов, определяющие переход триггера из одного состояния в другое. Если значение входного сигнала не влияет на данный переход, то в матрице указывается неопределенный коэффициент b. Для триггера D — V–типа дополнительно указан второй коэффициент по управляющему входу.
Таблица 3.1
Переходы 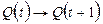 | Тип триггера | ||||||||
 | 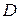 | 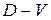 | 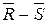 | 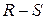 | |||||
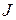 | 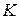 | 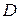 | 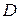 | 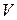 | 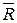 | 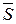 | 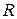 |  | |
| 0 – 0 | 0 | b | 0 | b | b a | b | 1 | b | 0 |
| 0 – 1 | 1 | b | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 – 0 | b | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 – 1 | b | 0 | 1 | b | b a | 1 | b | 0 | b |
Алгоритм структурного синтеза
1. Определяется необходимое число независимых шин управления. Число управляющих шин зависит от числа микроопераций, выполняемых устройством, и находится из соотношения 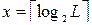 , где L — число микроопераций.
, где L — число микроопераций.
2. По числу различных состояний N устройства определяется необходимое количество триггеров: m 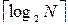 , каждое состояние устройства кодируется m-разрядным двоичным кодом, i-й разряд соответствует выходному сигналу i-го триггера.
, каждое состояние устройства кодируется m-разрядным двоичным кодом, i-й разряд соответствует выходному сигналу i-го триггера.
3. Кодируется внутреннее состояние синтезируемого автомата.
4. Согласно закону функционирования составляется кодированная таблица выходов устройства и переходов из одного состояния в другое при определенных входных воздействиях. Поскольку устройство представляет совокупность триггеров, такая таблица будет включать функции возбуждения всех входов триггеров возбуждения.
5. Выбирается (или задается) тип каждого триггера, по таблице переходов или матрице переходов составляются таблицы функций возбуждения всех входов каждого триггера.
6. Полученные функции возбуждения и функции выходов минимизируются соответствующим выбором значений неопределенных коэффициентов.
7. Согласно функциям возбуждения и в соответствии с выбранной (заданной) элементной базой строится структурная схема.
Синтез микропрограммных автоматов. Управляющий автомат, реализующий микропрограмму работы дискретного устройства, принято называть микропрограммным автоматом. Его синтез состоит из следующих этапов:
1. Составление частных содержательных микропрограмм выполнения операции автомата.
2. Построения частных микропрограмм с учетом отметок граф-схемы алгоритма символами.
3. Получение отмеченных частных микропрограмм.
4. Построение графов частных управляющих автоматов Мили или Мура.
5. Построения графа многофункционального автомата Мили или автомата Мура путем объединения состояний автоматов и введения настроечного алфавита.
6. Структурный синтез.
Далее составляется таблица переходов микропрограммного автомата. Для автомата Мили таблица содержит четыре столбца: am и as — исходное состояние и состояние перехода; х (am, as) — конъюнкция переменных из множества х, принимающая значение 1 на данном переходе; у (am, as) — подмножество выходных переменных, принимающих значение 1 на данном переходе. Каждая строка таблицы переходов соответствует одному пути перехода, т.е. дуге графа автомата с одним входным и одним выходным сигналами.
Таблица переходов микропрограммного автомата Мура содержит три столбца. В ней выходные сигналы из множества у (am) записываются в столбце am рядом с состоянием, в котором они формируются.
С помощью минимизации числа строк таблицы переходов автомата и методов доопределения функций строится логическая схема автомата, являющаяся совместной реализацией функций возбуждения функций выходов.
Абстрактный синтез автоматов. Задача абстрактного синтеза заключается в составлении таблиц переходов и выходов автомата по заданным условиям его функционирования.
Абстрактный синтез автоматов включает два этапа. Первый этап состоит в получении таблиц переходов и выходов в некоторой исходной форме. На втором этапе проводится минимизация количества внутренних состояний заданного автомата.
Алгоритм абстрактного синтеза заключается в следующем. Фиксируется начальное состояние a0 и для входного слова li, состоящего из r букв, назначается r внутренних состояний автомата ai1, ai2, …, air. Переходы в автомате назначаются так, что первая буква слова li переводит автомат из состояния a0 в состояние ai1, вторая буква — из состояния ai1 в состояние ai2 и т.д. Аналогичные последовательности внутренних состояний назначаются для всех остальных слов. Затем все конечные состояния air, в которые автомат попадает после подачи слов, входящих в событие Sj, отмечаются выходным сигналом уi.
Чтобы система переходов автомата была определенной для всех слов, имеющих одинаковые начальные отрезки, следует назначать одну и ту же последовательность состояний. В состояниях, не отмеченных буквами выходного алфавита у1, …, уk, а также в начальном состоянии автомат должен выдавать пустую букву, соответствующую событию Sk+1. Для запрещенного события последовательность состояний можно не назначать.
При абстрактном синтезе целесообразно использовать следующие соотношения: 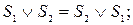
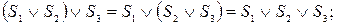
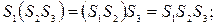
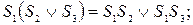
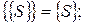
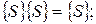
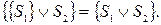
Алгоритм минимизации числа внутренних состояний автомата включает следующие действия:
1. Все внутренние состояния разбиваются на группы, количество которых равно количеству выходных сигналов автомата. Если существует такое состояние, в котором автомат выдает пустое слово, то такие состояния также выделяют в общую группу.
2. По таблице переходов автомата определяют, к каким группам принадлежат внутренние состояния, в которые автомат переходит из данного состояния под воздействием каждой буквы входного алфавита.
3. Проводится новое разделение внутренних состояний на группы, при этом объединяются в каждой группе состояния, отмеченные одинаковой последовательностью букв.
4. Пользуясь таблицей переходов автомата, снова отмечаются каждые состояния последовательности букв. Объединение состояний в группы продолжается до тех пор, пока новые группы состояний появляться не будут.
 |
| рис. 3.1 |
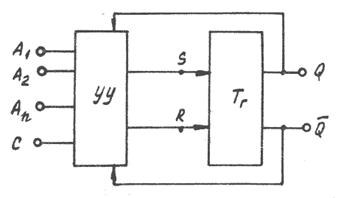
Триггерные устройства. Основными элементами, предназначенными для хранения информации, являются устройства с двумя устойчивыми состояниями — триггеры. Структуру триггера можно представить в виде запоминающего элемента и схемы управления (рис 3.1).
Запоминающий элемент имеет два выхода Q и 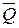 , разрешенные сигналы на которых всегда противоположны, и два входа s (set – установка) и r (reset – сброс). Переключающий сигнал по входу s устанавливает запоминающий элемент в состояние «1», а по входу r — в состояние «0». В общем случае запоминающий элемент может иметь несколько установочных входов.
, разрешенные сигналы на которых всегда противоположны, и два входа s (set – установка) и r (reset – сброс). Переключающий сигнал по входу s устанавливает запоминающий элемент в состояние «1», а по входу r — в состояние «0». В общем случае запоминающий элемент может иметь несколько установочных входов.
Схема управления преобразует информацию, поступающую на входы А1…Аn, в сигналы, которые подаются на установочные входы запоминающего элемента. Как правило, триггеры имеют еще один вход — вход для синхронизирующих сигналов С. Сигналы, поступающие на этот вход, определяют момент приема триггером входной информации. Поскольку прием информации синхронизирован с моментом подачи сигнала на вход С, то такой триггер назван синхронизируемым, или синхронным.
Рассматриваемые ниже триггеры обладают следующими свойствами. На входы А1…Аn поступают сигналы, несущие логическую входную информацию, на вход С — сигнал синхронизации. Входная информация принимается на хранение триггером с поступлением сигнала синхронизации или изменением его фронта. Такой режим соответствует синхронной работе триггера. Но синхронный триггер может применяться и при асинхронной работе. При этом на синхронизирующий вход триггера сигналы могут поступать от схем, непосредственно не связанных с синхронизирующими сигналами.
Наряду с хранением информации триггер может выполнять различные логические функции. Логические свойства триггера можно описать с помощью таблицы переходов (табл. 3.2), которая Q(t+1) определяет зависимость выходных сигналов триггера от значений входных сигналов Ai(t) и состояния триггера Q(t) в предыдущий момент времени. Для каждого типа триггера, задаваемого таблицей переходов, вводят специальное обозначение входов, отличное от общего обозначения А.
Таблица 3.2а. Таблица переходов триггера D
| Вход (время t) | Выход (время t+1) |
Таблица 3.2б. Таблица переходов триггеров J-K, R -S,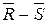
| Входы (время t) | Выход (время t+1) | |||
| 0 | 0 | Q(t) | Q(t) | - |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 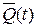 | - | 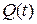 |
R, 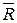 , K , K | S, 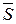 , J , J | J-K | R-S | 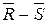 |
Рассмотрим наиболее часто применяемые типы триггеров.
D – триггер имеет один логический вход D (delay – задержка), состояние которого с каждым синхронизирующим сигналом передается на выход, т.е. выходные сигналы представляют собой задержанные входные. Таким образом, D – триггер — элемент задержки входных сигналов на один такт. Характеристическое уравнение триггера Q(t+1)=D(t).
J-K – триггер имеет два логических входа: j и k. Сигнал по входу j (j=1) устанавливает триггер в единичное состояние, а по входу k (k=1) в нулевое состояние. Если j=k=1, то триггер изменяет свое состояние на противоположное; при одновременной подаче на входы сигналов j=k=0 триггер не изменяет своего состояния. Характеристическое уравнение триггера  .
.
R-S – триггер имеет два логических входа: R и S. Одновременная подача на оба входа триггера сигналов, соответствующих единице, запрещена. Если на оба входа поданы сигналы, соответствующие нулю, то триггер на изменяет своего состояния. Характеристическое уравнение триггера 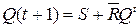 .
.
Обычно триггер, управляемый по синхронному входу, кроме информационных входов А имеет, как правило, асинхронные входы предварительной установки триггера в состояние «0» или «1». Сигналы, поступающие на эти входы, пользуются приоритетом, т.е. независимо от состояния других входов триггера они сразу (по переднему фронту) устанавливают триггер в определенное состояние. Буквой 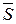 обозначают асинхронный вход для установки триггера в состояние «1», а буквой
обозначают асинхронный вход для установки триггера в состояние «1», а буквой 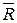 — для установки триггера в состояние «0». Синхронный триггер имеет обычно инверсные установочные входы и реализует функцию, приведенную в таблице переходов (см. табл. 3.2, б). Синхронные триггеры с асинхронными и установочными входами получили название универсальных триггеров соответствующего типа.
— для установки триггера в состояние «0». Синхронный триггер имеет обычно инверсные установочные входы и реализует функцию, приведенную в таблице переходов (см. табл. 3.2, б). Синхронные триггеры с асинхронными и установочными входами получили название универсальных триггеров соответствующего типа.
Синтез триггерных устройств. Универсальные триггеры классифицируются по способу их построения на два основных типа: основной — вспомогательный (M – S) со срабатыванием по заднему фронту сигнала синхронизации и основной — коммутирующий (М – К) со срабатыванием по переднему фронту сигнала синхронизации. Исходными данными при разработке триггера служат заданные описания его логического функционирования и требования к основным электрическим параметрам. Общая методика синтеза триггерных устройств следующая:
1. Составление таблицы переходов. Функционирование триггера может быть задано в различной форме: словесным описанием, в виде временных диаграмм, таблицами состояний и т.п. Входной алфавит определяется типом проектируемого триггера, а выходной алфавит и функции выходов выбираются двоичные. При структурном проектировании в качестве исходной информации о функционировании триггера используют таблицы переходов.
2. Составление кодированной таблицы прямых выходов триггера и его функций возбуждения, исходя из заданного типа базового триггера и кодирования его внутренних состояний.
3. Минимизация полученных функция возбуждения и выходов.
4. Составление структурной схемы на основании минимальных функций возбуждения и выходов в соответствии с выбранной элементной базой.
5. Составление электрической схемы триггера.
Синтез M – S-триггера. При синтезе M – S-триггеров с некоторыми ограничениями можно применить общую теорию конечных автоматов. Входной алфавит определяется типом проектируемого триггера, а выходной алфавит и функции выходов — двоичные. Для такого триггера закодированные внутренние состояния (Si) автомата приведены в табл. 3.3, 3.4.
Таблица 3.3.
| Si | M | S |
| S0 | ||
| S1 | ||
| S2 | ||
| S3 |
Таблица 3.4.
| Pi | C | V | K |
| P0 | |||
| P1 | |||
| P2 | |||
| P3 | |||
| P4 | |||
| P5 | |||
| P6 | |||
| P7 |
Таблица 3.5.
| Pi | Si | |||
| S0 | S1 | S2 | S3 | |
| P0 | S0 | S0 | S3 | S3 |
| P1 | S0 | S0 | S3 | S3 |
| P2 | S0 | S0 | S3 | S3 |
| P3 | S0 | S0 | S3 | S3 |
| P4 | S0 | — | — | S3 |
| P5 | S0 | S1 | — | S1 |
| P6 | S2 | — | S2 | S3 |
| P7 | S2 | — | — | S1 |
Таблицы переходов и синтез двухступенчатого триггера рассмотрим на примере синхронного J-K – триггера, собранного на базе бистабильных ячеек 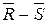 и логических схем И — НЕ. Закодированные слова, подаваемые на входы триггера, приведены в табл. 3.6. С помощью таблицы кодирования внутренних состояний и входных слов составляется таблица переходов синхронного триггера. При отсутствии синхросигнала (по его заднему фронту) происходит перезапись состояния первой ступени М-триггера во вторую ступень S-триггера. Если на вход С подается сигнал синхронизации, то перезапись по переднему фронту из М в S запрещается. Таким образом, входные слова Р0…Р3 оказывают на автомат одинаковое воздействие.
и логических схем И — НЕ. Закодированные слова, подаваемые на входы триггера, приведены в табл. 3.6. С помощью таблицы кодирования внутренних состояний и входных слов составляется таблица переходов синхронного триггера. При отсутствии синхросигнала (по его заднему фронту) происходит перезапись состояния первой ступени М-триггера во вторую ступень S-триггера. Если на вход С подается сигнал синхронизации, то перезапись по переднему фронту из М в S запрещается. Таким образом, входные слова Р0…Р3 оказывают на автомат одинаковое воздействие.
Прочерком в таблице переходов (табл. 3.5) обозначены избыточные состояния. Так, если автомат находится в состоянии S1 или S2, то слово Р4 не может быть подано на вход, потому что не произошла перезапись из М в S. Длительность синхросигнала должна быть достаточной для того, чтобы произошла перепись информации из М в S, по той же причине на вход не попадаются слова: Р5, если автомат находится в состоянии S2; Р6, если автомат находится в состоянии S1; Р7, если автомат находится в состоянии S1 или S2.
Таблица 3.6.
| Выходные сигналы | Функции возбуждения | |||||||||
| C | J | K | Q1(t) | Q2(t) | Q1(t+1) | Q2(t+1) | 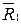 | 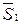 | 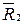 | 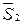 |
| x | x | b | b | |||||||
| b | ||||||||||
| b | ||||||||||
| b | b | |||||||||
| b | b | |||||||||
| — | — | — | — | — | — | |||||
| — | — | — | — | — | — | |||||
| b | b | |||||||||
| b | b | |||||||||
| b | b | |||||||||
| — | — | — | — | — | — | |||||
| b | ||||||||||
| b | ||||||||||
| — | — | — | — | — | — | |||||
| b | b | |||||||||
| b | b | |||||||||
| b | ||||||||||
| — | — | — | — | — | — | |||||
| — | — | — | — | — | — | |||||
| b |
Однако допустима подача входного слова Р5, если автомат находится в состоянии S1, и входного слова Р6, когда автомат находится в состоянии S2, так как в этом случае М находится в нулевом состоянии.
По таблице переходов составляется кодированная таблица переходов и функций возбуждения J-K – триггера (таблица 3.6), по которой находятся функции возбуждения по каждому входу триггеров, при этом используются любые методы минимизации.
Функция возбуждения
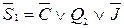 ;
; 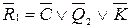 ;
; 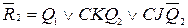 ;
; 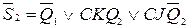
или в базисе И—НЕ
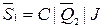 ;
;
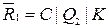 ;
;  ;
; 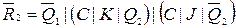
Структурная схема J-K – триггера приведена на рисунке 3.2.
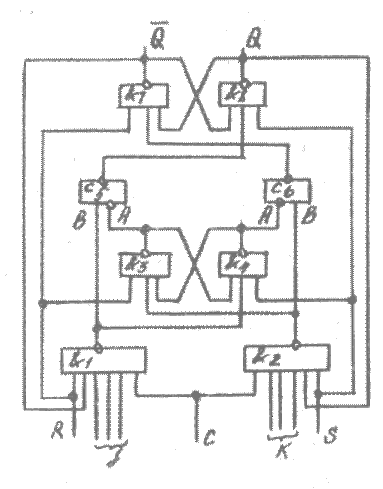
Рис. 3.2 J-K – триггер
| Таблица 3.7 Таблица истинности схем И—НЕ5 и И—НЕ6 | |||||||||||||||
|
Универсальный триггер типа J-K собран по структуре M – S на схемах И—НЕ (рис. 3.2). Основной триггер М, собранный на И—НЕ3 и И—НЕ4, принимает входную информацию и переключается по переднему фронту сигнала С.
По заднему фронту сигнала С информация из основного триггера М переписывается во вспомогательный триггер S, собранный на схемах И—НЕ7 и И—НЕ8, где фиксируется состояние триггерного устройства. Триггер имеет встроенные трехвходовые логические схемы И по входам J и K.
Рассмотрим синхронный режим работы универсального триггера J-K при подаче на его входы J и K одновременно единичных сигналов. Будем считать, что триггер находится в нулевом состоянии, т.е. на его входах 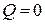 и
и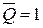 на входы
на входы 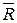 и
и 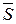 постоянно поданы единичные сигналы.
постоянно поданы единичные сигналы.
При одновременном поступлении единичных сигналов J, K и С на всех входах схемы И—НЕ1 (с учетом единичного сигнала 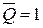 ) будут присутствовать единичные сигналы, которые переключают схему в нулевое состояние. Это, в свою очередь приведет к переключению схемы И—НЕ4 в единичное состояние. Единичный сигнал с выхода этой схемы поступает на одни из входов схемы И—НЕ3, на другие ее входы подаются единичные сигналы с входа
) будут присутствовать единичные сигналы, которые переключают схему в нулевое состояние. Это, в свою очередь приведет к переключению схемы И—НЕ4 в единичное состояние. Единичный сигнал с выхода этой схемы поступает на одни из входов схемы И—НЕ3, на другие ее входы подаются единичные сигналы с входа 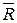 и с выхода схемы И—НЕ2. Таким образом, оказывается, что на все входы схемы И—НЕ3 поданы единичные сигналы, которые переключают схему в нулевое состояние, и на выходе основного триггера М записывается единичный сигнал. В этот момент на триггере М фиксируется информация, противоположная информации, содержащейся на триггере S. Перепись этой информации во вспомогательный триггер S при наличии синхронизирующего сигнала невозможна, так как на оба входа логических схем с инверсным входом И—НЕ5 и И—НЕ6 подаются одинаковые входные сигналы (на схему И—НЕ5 — нулевые, на схему И—НЕ6 — единичные), которые сохраняют на их выходах единичные состояния (работа логической схемы с инверсным входом поясняется табл. 3.7).
и с выхода схемы И—НЕ2. Таким образом, оказывается, что на все входы схемы И—НЕ3 поданы единичные сигналы, которые переключают схему в нулевое состояние, и на выходе основного триггера М записывается единичный сигнал. В этот момент на триггере М фиксируется информация, противоположная информации, содержащейся на триггере S. Перепись этой информации во вспомогательный триггер S при наличии синхронизирующего сигнала невозможна, так как на оба входа логических схем с инверсным входом И—НЕ5 и И—НЕ6 подаются одинаковые входные сигналы (на схему И—НЕ5 — нулевые, на схему И—НЕ6 — единичные), которые сохраняют на их выходах единичные состояния (работа логической схемы с инверсным входом поясняется табл. 3.7).
По окончании действия сигнала синхронизации состояние схемы И—НЕ1 изменяется на единичное, схема И—НЕ5 переходит в нулевое состояние, которое переключает схему И—НЕ8 в единичное состояние. Единичный сигнал, поступающий на вход схемы И—НЕ7, переключает ее в нулевое состояние.
Следовательно, схемы И—НЕ5 и И—НЕ6 служат устройством управления перезаписи информации из основного триггера М во вспомогательный триггер S. Задержка при переключении схемы из одного устойчивого состояния в другое составляет 4td.
При подаче сигнала только на вход С при условии, что на всех остальных входах подан сигнал единица, триггер работает в счетном режиме, т.е. аналогично вышеописанному режиму.
По асинхронным 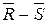 входам триггер управляется аналогично асинхронным входам триггера D–типа. Поступающий на вход синхронизации нулевой сигнал С=0 блокирует переключение основного триггера М, а входные нулевые сигналы
входам триггер управляется аналогично асинхронным входам триггера D–типа. Поступающий на вход синхронизации нулевой сигнал С=0 блокирует переключение основного триггера М, а входные нулевые сигналы 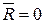 или
или 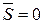 переключают только вспомогательный триггер S. На основе триггера J-K можно, применяя соответствующую коммутацию или используя дополнительные схемы, получить триггеры, выполняющие функции триггеров R-S, D и Т.
переключают только вспомогательный триггер S. На основе триггера J-K можно, применяя соответствующую коммутацию или используя дополнительные схемы, получить триггеры, выполняющие функции триггеров R-S, D и Т.
Синтез М – К триггера. Рассмотрим особенности структурного проектирования триггеров класса М – К на примере синхронизируемого фронтом D–триггера, используя элементы И—НЕ.
Закодированные входные слова, подаваемые на вход автомата, представлены в табл. 3.8.
Для кодирования четырех состояний достаточно двух переменных Q1 и, однако выберем для кодирования внутренних состояний три переменные Q1, Q2, Q3 (табл. 3.9). Состояние схемы закодируем таким образом, чтобы выход схемы Q соответствовал выходу схемы Q1. При этом из четырех избыточных состояний два (S1 и S2) применены в качестве рабочих промежуточных состояний триггера. Пятое состояние используется промежуточным при переключении триггера из (3) → (2), а шестое — при переходе триггера из (1) → (4).
Таблица 3.8
| Pi | C | D |
| P1 | ||
| P2 | ||
| P3 | ||
| P4 |
Таблица 3.9
| Si | Q1 | Q2 | Q3 |
| S7 | |||
| S6 | |||
| S2 | |||
| S1 | |||
| S8 | |||
| S4 | |||
| S5 | |||
| S3 |
Введение этих промежуточных состояний позволило исключить критические гонки между системами обратных связей на всех переходах триггера. При заполнении таблицы переходов (табл. 3.10) примем, что триггер переключается по переднему фронту С и одновременное изменение сигналов C и D запрещено. Запрещенное состояние обозначается прочерком. По таблице переходов составляется кодированная таблица переходов и функций возбуждения D–триггера (табл. 3.11).
Таблица 3.10
| Pi | Si | |||||
| S1 | S2 | S3 | S4 | S5 | S6 | |
| P1 | S1 | S1 | S3 | S3 | — | — |
| P2 | S1 | S1 | S3 | S3 | — | — |
| P3 | S6 | S2 | S4 | S4 | — | S4 |
| P4 | S2 | S2 | S5 | S4 | S2 | — |
| Q | — | — |
Таблица 3.11
| Q(t) – Q(t+1) | 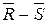 |
| 0 — 0 | b 1 |
| 0 — 1 | b 0 |
| 1 — 0 | 0 1 |
| 1 — 1 | 1 / b |
| b / 0 |
Данные табл. 3.12 заносятся на карты Вейча и производится минимизация функций. В результате получаем следующие минимальные функции возбуждения: 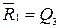 ;
; 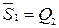 ;
; 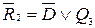 ;
; 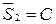 ;
; 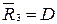 ;
; 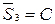 .
.
Реализованный по этим соотношениям триггер будет содержать цепи со статическим сбоем при некоторых переключениях сигналов. Для исключения статического риска необходимо заменить минимальные выражения 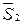 и
и 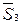 оптимальными
оптимальными 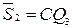 и
и 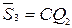 и ввести дополнительные третьи входы в элементы И — НЕ2 и И — НЕ3. Соединив между собой в соответствии с логическими выражениями основной и коммутирующий триггеры, получим схему D–триггера в базисе И — НЕ (рис. 3.3).
и ввести дополнительные третьи входы в элементы И — НЕ2 и И — НЕ3. Соединив между собой в соответствии с логическими выражениями основной и коммутирующий триггеры, получим схему D–триггера в базисе И — НЕ (рис. 3.3).
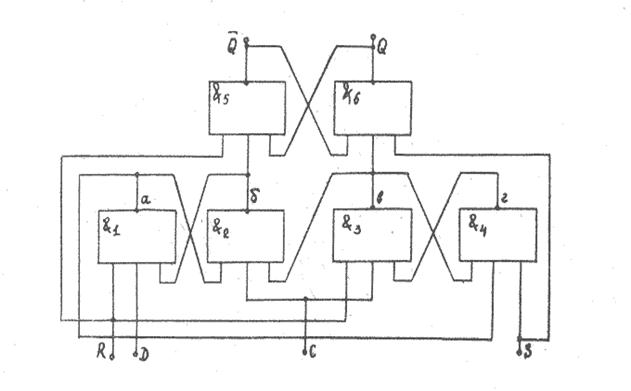
Рис. 3.3 D-триггер
Таблица 3.12
| С | D | Значения выходных сигналов | Функции возбуждения | ||||||||||
| Q1(t) | Q2(t) | Q3(t) | Q1(t+1) | Q2(t+1) | Q3(t+1) | 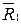 | 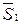 | 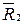 | 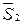 | 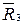 | 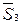 | ||
| — | — | — | — | — | — | — | — | — | |||||
| — | — | — | — | — | — | — | — | — | |||||
| b | 1/b | b/0 | b | ||||||||||
| b | 1/b | b/0 | 1/b | b/0 | |||||||||
| — | — | — | — | — | — | — | — | — | |||||
| b | b | 1/b | b/0 | ||||||||||
| — | — | — | — | — | — | — | — | — | |||||
| b | 1/b | b/0 | 1/b | b/0 | |||||||||
| — | — | — | — | — | — | — | — | — | |||||
| — | — | — | — | — | — | — | — | — | |||||
| b | 1/b | b/0 | b | ||||||||||
| b | 1/b | b/0 | 1/b | b/0 | |||||||||
| — | — | — | — | — | — | — | — | — | |||||
| b | b | 1/b | b/0 | ||||||||||
| — | — | — | — | — | — | — | — | — | |||||
| b | 1/b | b/0 | 1/b | b/0 | |||||||||
| — | — | — | — | — | — | — | — | — | |||||
| b | 1/b | b/0 | |||||||||||
| b | 1/b | b/0 | b | ||||||||||
| b | 1/b | b/0 | |||||||||||
| — | — | — | — | — | — | — | — | — | |||||
| b | b | 1/b | b/0 | ||||||||||
| — | — | — | — | — | — | — | — | — | |||||
| b | 1/b | b/0 | |||||||||||
| — | — | — | — | — | — | — | — | — | |||||
| — | — | — | — | — | — | — | — | — | |||||
| b | 1/b | b/0 | b | ||||||||||
| b | 1/b | b/0 | |||||||||||
| — | — | — | — | — | — | — | — | — | |||||
| b | b | 1/b | b/0 | ||||||||||
| 1/b | b/0 | b | |||||||||||
| b | 1/b | b/0 |
Универсальный синхронный триггер типа D с инверсными установочными входами 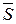 и
и 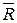 функционирует согласно таблице переходов (табл. 3.13).
функционирует согласно таблице переходов (табл. 3.13).
Таблица 3.13
Таблица переходов триггера D
| Входные сигналы (время t) | Время Q(t+1) | Функция триггера | ||
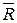 | 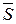 | С | ||
| — | Не определена | |||
| Уст. «0» | ||||
| Уст. «1» | ||||
| Q(t) | Хранение Q(t) | |||
| D(t) | Задержка D(t) |
В отсутствие сигналов логического нуля на установочных входах данный триггер при С=0 не меняет своего состояния, при С=1 запоминает (задерживает) сигнал, поданный на управляющий вход D.
Схема триггера (рис3.3) реализована на элементах И—НЕ; запоминающий элемент образован на И—НЕ5 и И—НЕ6; остальные элементы составляют схему управления триггера с входными сигналами «б» и «в». Функции элементов И—НЕ: 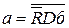 ;
; 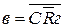 ;
; 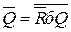 ;
; 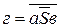 ;
;  .
.
В асинхронном режиме нулевое значение синхросигнала С=0 приводит к отключению схемы управления (б=в=1) от запоминающего элемента, т.е. 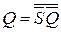 и
и 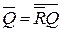 . Работа триггера определяется только установочными сигналами:
. Работа триггера определяется только установочными сигналами:
при 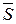 =
=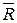 =0 вызывает Q=1 и
=0 вызывает Q=1 и 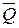 =1, т.е. схема функционирует неправильно;
=1, т.е. схема функционирует неправильно;
при 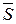 =
=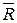 =1 запоминающий элемент сохраняет прежнее состояние;
=1 запоминающий элемент сохраняет прежнее состояние;
при 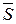 = 0 и
= 0 и 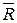 =1 триггер либо сохраняет единичное состояние, либо переходит в него, если предыдущее состояние было нулевым;
=1 триггер либо сохраняет единичное состояние, либо переходит в него, если предыдущее состояние было нулевым;
при 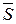 =1 и
=1 и 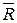 =0 триггер либо сохраняет нулевое состояние, либо переходит в него, если прежнее состояние было единичным (табл. 3.14). Время срабатывания триггера Ттр=2τэл.
=0 триггер либо сохраняет нулевое состояние, либо переходит в него, если прежнее состояние было единичным (табл. 3.14). Время срабатывания триггера Ттр=2τэл.
Таблица 3.14
Асинхронный режим триггера D
| Время | 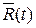 | 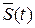 | 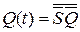 | 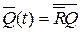 |
| t0 | 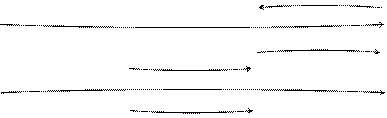 1 1 | |||
| t1 | ||||
| t2 | ||||
| t3 | ||||
| t4 | ||||
| t5 |  1 1 | |||
| t6 | 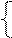 0 0 |
Состояние триггера в момент t6 (при снятии запрещенных входных сигналов 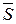 =
=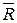 =0) будет «0» или «1» в зависимости от случайных процессов в схеме. Временная работа триггера типа D приведена на рис. 3.4.
=0) будет «0» или «1» в зависимости от случайных процессов в схеме. Временная работа триггера типа D приведена на рис. 3.4.

Рис. 3.4
В синхронном режиме на установочных входах рабочие сигналы отсутствуют: 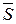 =
=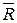 =1 и функции элементов И—НЕ схемы имеют вид
=1 и функции элементов И—НЕ схемы имеют вид 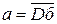 ;
; 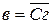 ;
; 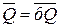 ;
; 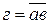 ;
;  , т.е. состояние запоминающего элемента определяется сигналами «б» и «в» с выходов схемы управления. При отсутствии синхросигнала С=0 запоминающий элемент не меняет своего состояния; при наличии синхросигнала состояние триггера определяется ранее поданным сигналом управления по входу D (табл. 3.15).
, т.е. состояние запоминающего элемента определяется сигналами «б» и «в» с выходов схемы управления. При отсутствии синхросигнала С=0 запоминающий элемент не меняет своего состояния; при наличии синхросигнала состояние триггера определяется ранее поданным сигналом управления по входу D (табл. 3.15).
Таблица 3.15
Синхронный режим триггера D
| Время | D(t) | C(t) | 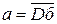 | 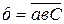 | 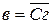 | 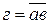 | 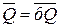 |  |
| t0 |  - - | - | - | |||||
| t1 | ||||||||
| t2 | < |
|
|

 2014-02-02
2014-02-02 1023
1023