.
Из полученного выражения видно, что для реализации этой функции необходимо 6 элементов «И-НЕ».
То же самое проводим для 2-й формы МДНФ:
 .
.
Однако число элементов «И-НЕ» в структурной схеме можно уменьшить, если вместо МДНФ функции использовать сокращенную ДНФ ее, т.е. ввести в выражение ДНФ функции обе необязательные импликанты:
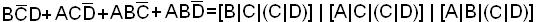 .
.
Требуется 5 элементов (рис.3).
2. Определим МКНФ функции с помощью обратной функции:
f(ABCD)=m0+ m1+m2+ m3+m4+ m6+ m7+ m8+ m9+ m11+ m15;

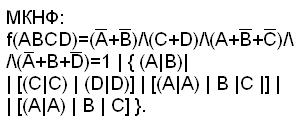
Рис.3.
Мультиплексором называют устройства, которые позволяют реализовать логическую схему любой сложности. В отличие от интегральных схем, где имеется набор элементов, обладающих большой избыточностью, мультиплексор совмещает логические функции в модуле одного типа. Так как такой модуль выполнен в виде одного кристалла интегральной схемы (ИС), то он обладает более высоким быстродействием и надежностью, облегчает проектирование и упрощает компоновку печатной платы. При изготовлении мультиплексоров, можно использовать технологию средних интегральных схем для размещения на одном кристалле законченных функциональных логических схем (счетчики, дешифраторы, сдвиговые регистры и др.). При этом один тип модуля может обеспечить проектирование различных узлов одного изделия, а также различные изделия на одном и том же типе элементов. Мультиплексор в принципе может быть реализован на любых элементах, применяемых в схемотехнике: элементы диодно-транзисторной логики, транзисторно-транзисторной логики или любой другой. В настоящее время получили распространение два типа модулей: сдвоенные четырехвходовые (рис.4.а) и восьмивходовые (рис.4.б).
Основные характеристики рассматриваемых мультиплексоров приведены в табл.23.
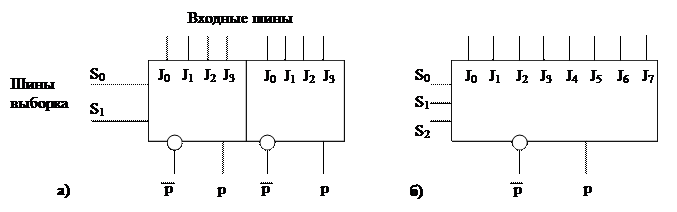
Рис.4.
Таблица 23.

Структурная схема мультиплексора приведена на рис.5. Эта схема собрана из элементов «И-НЕ» и имеет М=2n-1, F=2n-1+n+1.
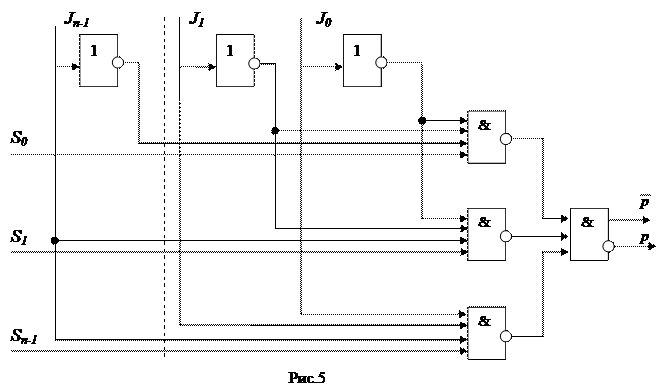 |
Из основных положений построения логических схем можно показать, что для реализации любой булевой функции n переменных достаточно иметь устройство, которое содержит 2n-1 схемы, реализующие соответствующим образом подобранные 2n-1 минтермов. Если функция обращается в единицу на числе наборов больше чем 2n-1, то нетрудно показать, что в этом случае будут обязательно склеивающиеся минтермы и, следовательно, потребуется меньшее количество оборудования. Исходя из этих предпосылок можно организовать внутреннюю структуру мультиплексора. Половина четырехвходового мультиплексора может реализовать любую из 256 функций трех аргументов (рис.4,а). При этом на шины выборки подаются сигналы двух любых аргументов, а на входные шины соответствующие сигналы третьего аргумента.
Предположим, что на мультиплексорах надо реализовать один разряд комбинационного сумматора на три входа. Так как в комбинационном сумматоре необходимо иметь значение суммы в данном разряде и значение переноса в последующий старший разряд, то целесообразно использовать сдвоенный четырехвходовой мультиплексор. Булево уравнение для функции суммы будет
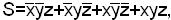
для переноса 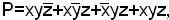
где S –сумма в данном разряде;
x, y –значения слагаемых в данном разряде;
z – перенос из предыдущего младшего разряда;
P – перенос в последующий старший разряд.
На основе булевых уравнений составляются таблицы истинности заданных функций и карты минимизации (рис.6,а,б).
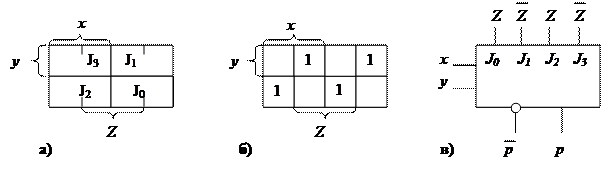 |
Рис.6.
Карта Вейча могла быть составлена и без таблицы истинности непосредственно по формуле. Таблица истинности или карта минимизации используется для определения сигналов трех переменных к мультиплексору.
 2014-02-02
2014-02-02 2775
2775








