Уравнение Гиббса связывает величину адсорбции со способностью растворенного вещества изменять поверхностное натяжение. Выводится из объединенного уравнения I и II законов термодинамики для внутренней энергии поверхностного слоя.
dQ = dU + pdV,
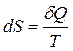 , откуда dQ = ТdS.
, откуда dQ = ТdS.
Объединим оба закона
dU + pdV = ТdS.
Поскольку при адсорбции ПАВ на границе раздела жидкость-газ объем системы остается неизменным, pdV = 0. Тогда
dU = ТdS. (2)
В результате адсорбции происходит перераспределение компонентов между объемом фазы и поверхностным слоем, что приводит к изменению их химических потенциалов. Поэтому уравнение (2) необходимо дополнить двумя составляющими, характеризующими химическую и поверхностную энергии
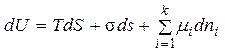 , (3)
, (3)
где s – поверхностное натяжение раствора; s – суммарная поверхность раздела фаз; mi – химический потенциал i -го компонента в поверхностном слое; dni – бесконечно малое изменение концентрации i -го компонента в поверхностном слое.
Уравнение (3) – дифференциальное уравнение первой степени относительно экстенсивных величин, стоящих под знаком дифференциала (S, s, ni), Согласно теореме Эйлера, такое уравнение можно интегрировать при постоянных значениях коэффициентов (интенсивных величин), т.е.
 . (4)
. (4)
Рассматривая теперь любые возможные изменения системы, т.е. дифференцируя (4), получим
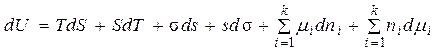 . (5)
. (5)
Вычтем из (5) уравнение (3)
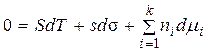 . (6)
. (6)
Для изотермического процесса Т = const, SdT = 0.
Разделим обе части (6) на s:
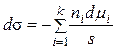 .
.
Отношение ni/s = Гi – избыток компонента i в поверхностном слое по сравнению с его концентрацией в объеме фазы – избыточная (гиббсовская) адсорбция, тогда
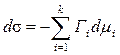 . (7)
. (7)
Уравнение (7) – фундаментальное адсорбционное уравнение Гиббса.
Для двухкомпонентной системы, состоящей из растворителя 1 и растворенного вещества 2 уравнение (7) запишется
– d s = Г 1 dm 1 - Г 2 dm 2.
Если Г 1 << Г 2
– d s = Гdm.. (8)
Поскольку уравнение (8) записано для одного компонента, индекс 2 можно опустить.
Химический потенциал компонента m можно выразить через стандартный химический потенциал m* и активность компонента а:
m = m* + RT ln a,
dm = RTd ln a = RT 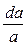 ,
,
 .
.
Для небольших концентраций
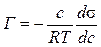 . (9)
. (9)
При высоких концентрациях
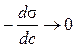 ,
,
следовательно, уравнение Гиббса не описывает всю изотерму адсорбции, т.е. не работает при больших концентрациях.
Практическое значение уравнения Гиббса состоит в том, что с его помощью можно рассчитать адсорбцию по результатам измерения поверхностного натяжения.
Непосредственно адсорбцию, т.е. количество вещества, содержащееся в поверхностном слое, можно определить методом меченых атомов или методом молекулярных срезов (когда с поверхности раствора с помощью прибора, напоминающего микротом, срезается очень тонкий слой жидкости и в нем определяется количество компонента). Методы эти очень трудоемки.
На практике адсорбцию определяют, устанавливая зависимость поверхностного натяжения раствора s от концентрации ПАВ с.
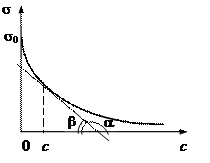
Для расчета адсорбции по уравнению Гиббса необходимо при данной равновесной концентрации с найти значение производной (рис. 10):
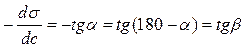 .
.
|
Значение производной можно найти также дифференцированием аналитического уравнения, описывающего зависимость поверхностного натяжения от концентрации ПАВ.
 2014-02-02
2014-02-02 17658
17658
