Механизмы стимулирования снижения издержек

Многоканальные механизмы

В автоматизированных системах управления технологическими процессами (АСУ ТП) широко применяются так называемые «советчики оператора». По сути дела, это – компьютерная программа, которая моделирует технологический процесс и после определенного периода обучения дает советы оператору по управлению процессом. На практике эффективность таких пассивных советчиков оказалась невысокой. Дело в том, что в период обучения советы компьютерной программы были не всегда хорошими, и опытный оператор переставал их воспринимать, хотя со временем управление, предлагаемое «советчиком» в штатных ситуациях, часто было лучше, чем управление оператора. Необходимо было предложить механизм, побуждающий оператора прислушиваться к рекомендациям «советчика». Были разработаны так называемые пересчетные модели, которые могли предсказать по результатам выход процесса: что было бы, если бы оператор принял рекомендации «советчика». Если рекомендации «советчика» приводили к лучшему результату, то оператор штрафовался, а если управление оператора было лучше чем рекомендации «советчика», то оператор премировался. Фактически было организовано соревнование между оператором и советчиком оператора. При внедрении таких «активных советчиков оператора» ситуация изменилась. Оператор стал во многих случаях следовать рекомендациям модели, особенно в штатных ситуациях. Внедрение таких двухканальных механизмов в черной металлургии дало значительный экономический эффект.

Описанный двухканальный механизм можно обобщить в различных направлениях. Во-первых, можно использовать не один советующий канал, а несколько (многоканальные механизмы), например, используя различные модели и методы моделирования. Во-вторых, такие активные советчики можно применять не только при управлении технологическими системами, но и в управлении социально-экономическими системами (советчик генерального директора, советчик министра и возможно даже Президента).

Рассмотрим предприятие, состоящее из n подразделений. Поставим задачу разработки плана снижения издержек на определенную величину R [1,6]. Обозначим x_i – план снижения издержек для i -го подразделения. Снижение издержек требует затрат на проведение соответствующих мероприятий. Обозначим через:

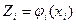, (3.21)

затраты i -го подразделения на проведение мероприятий по снижению издержек на величину x_i.

Примем, что:

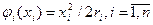. (3.22)

Рассмотрим следующий механизм стимулирования снижения издержек (который очень похож на механизм распределения заказов в корпорации – см. раздел 3.1). Подразделение получает средства h_i из централизованного фонда прямо пропорционально величине издержек x_i, то есть:

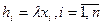, (3.23)

где 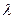– норматив, общий для всех подразделений.

Формирование плана снижения издержек происходит на основе сообщаемых подразделениями оценок функций затрат. Примем, что каждое подразделение сообщает оценку s_i коэффициента r_i функции затрат (3.22). План x ={ x_i } определяется по формуле:

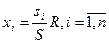, (3.24)

где 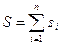, а норматив 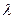равен:

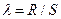. (3.25)

Проведем исследование описанного механизма. В качестве целевых функций подразделений примем разность средств, полученных из централизованного фонда, и затрат на проведение мероприятий по снижению издержек:

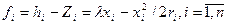. (3.26)

Подставляя в (3.26) выражения (3.24) и (3.25), получаем:

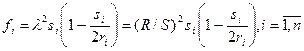(3.27)

Заметим, что при достаточно большом числе подразделений влияние оценки s_i отдельного подразделения на норматив 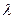сравнительно малό. Поэтому достаточно обоснованным представляется предложение о том, что при сообщении оценки s_i предприятие не учитывает этого влияния (так называемая гипотеза слабого влияния). В этом случае максимум целевой функции (3.27) достигается при сообщении оценки: 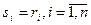, то есть при сообщении достоверной информации о функции производственных издержек.

Если в корпорации имеется предприятие с относительно большой величиной коэффициента r_i, то для этого предприятия гипотеза слабого влияния уже не имеет места. Пусть это предприятие с номером 1, r₁>H-r ₁, то есть r₁>H/2. Для остальных предприятий гипотеза слабого влияния является достаточно обоснованной, и поэтому 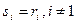. Обозначим H ₁= H-r ₁.

Для первого предприятия имеем: 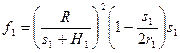. Максимизируя по s ₁, получаем:

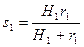. (3.28)

Если r ₁>> H ₁, то есть первое предприятие является фактически монопольным предприятием в области снижения издержек, то 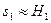, то есть монопольное предприятие сообщает оценку s₁ равную сумме коэффициентов r_i остальных предприятий.