2014-02-02
676
Частотные характеристики разомкнутых импульсных систем
Для того, чтобы получить выражение для АФЧХ импульсной системы, нужно в передаточную функцию этой системы подставить р = jv, где v =wТ - относительная частота.
Если передаточная функция разомкнутой импульсной системы в общем случае имеет вид:
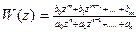, то выражение для АФЧХ (с учетом, что z = epT) имеет вид:
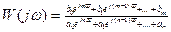. (11.1)
АФЧХ можно представить в виде суммы вещественной и мнимой частей W(jv) = U(v) + jV(v) или в показательной форме W(jv) = A(v)e jj(v), где
A(v) =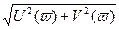 
- модуль АФЧХ,
j(v) = arctgV(v)/U(v) – аргумент АФЧХ.
Модуль АФЧХ равен отношению амплитуд решетчатых гармонических функций на выходе и входе импульсной системы в установившемся режиме колебаний, а аргумент АФЧХ - сдвигу фаз между этими решетчатыми функциями.
Как и у непрерывных систем, А(v) представляет амплитудно - частотную характеристику (АЧХ) импульсной системы, а j(v) -фазовую частотную характеристику (ФЧХ).
Отметим основные свойства частотных характеристик импульсных систем
1.Частотные характеристики импульсной системы (ЧХИС) обладают свойством периодичности, т. е. они являются периодическими функциями относительной частоты v с периодом повторения 2p.
Поэтому при построении ЧХИС достаточно ограничиться участком характеристики, соответствующим изменению частоты в диапазоне 2p, например, от v = -p до v= +p. Если принять во внимание, что участки ЧХИС в диапазоне изменения v от -p до 0 и от 0 до +p симметричны, то можно ограничиться построением ЧХ в диапазоне изменения v от 0 до p.
2. АФХ разомкнутой импульсной системы начинается и заканчивается на вещественной оси
3. В отличие от непрерывной системы ИС имеет множество частотных характеристик, соответствующих различным значениям параметра между точками квантования.
