Свойства математического ожидания.
Пример.
| Х | ||||||
| p | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
М[Х]=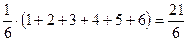 .
.
М[Х]=  - для непрерывной случайной величины.
- для непрерывной случайной величины.
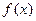 плотность распределения.
плотность распределения.
1. М[С]=С (С – постоянная).
2. М[СХ]=С М[Х].
3. Если есть две случайные величины: Х и Y, то М[Х+ Y]= М[Х]+ +М[Y].
4. Если есть две независимые случайные величины: Х и Y, то М[ХY]=М[Х]М[Y].
Дисперсия – число, которое характеризует степень отклонения случайной величины от её среднего значения (математического ожидания). Определяется как средний квадрат отклонения случайной величины.
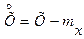 - отклонение случайной величины от её среднего значения
- отклонение случайной величины от её среднего значения
D[X] = М[  2 ]=М[(
2 ]=М[(  )2 ]= =М[
)2 ]= =М[ 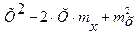 ]=М[
]=М[ 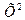 ]
] 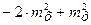 = М[
= М[ 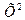 ]-
]-  .
.
Если случайная величина задана в виде таблицы, то
D[X] = .
.
Для непрерывной случайной величины:
D[X] =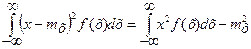 .
.
 2014-02-02
2014-02-02 550
550








