Равномерный закон распределения случайной величины

Случайная величина Х распределена равномерно на отрезке , еслиона имеет плотность вероятности вида:

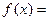С, если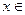

и

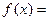0, если .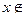

Нормальный закон распределения случайной величины (закон Гаусса).

Случайная величина распределена нормально,еслиона имеет функцию плотности вероятности вида:

.

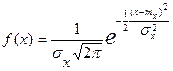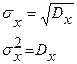
Нормальный закон широко используется в практической деятельности в силу теоремы, в соответствии с которой сумма случайных величин при увеличении числа слагаемых распределена нормально даже в том случае, если слагаемые имеют распределение, отличное от нормального.

В практической деятельности на результат воздействует множество факторов.

Стандартная форма нормальногозакона распределения.

Случайная величина Х приводится к безразмерному виду путём её нормировки на величину стандартного отклонения 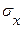. Помимо этого, желательно сместить математическое ожидание в начало координат.

Переходят к случайной величине Z следующим образом:

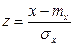
При этомсправедливо:

М[Z]= 0, D [Z]=1

Тогда стандартная форма нормального закона распределения -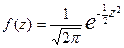

1. Плотность вероятности симметрична относительно оси ординат.

2. .

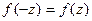3. F(x)=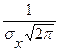

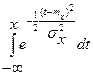
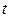- переменная интегрирования.

Для вычислительных целей используется функция Лапласа

.

Функция Лапласа связана с функцией распределения следующим образом:

F(z)=0,5+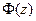

=

=

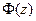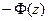
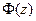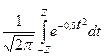
Распределение «хи-квадрат».

Рассматриваются случайные величины , , …, .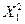

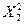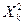Случайная величина 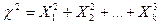называется хи-квадрат.

При этом случайные величины 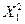, , 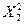…, 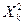распределены нормально с параметрами N (0, 1).

Закон распределения случайной величины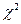называется 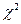- распределением с k степенями свободы.

С увеличением k закон распределения случайной величины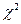стремится к нормальному распределению.

Закон 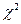называется предельным.