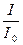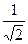Чтобы определить частотные свойства нужно решить следующие задачи:
1) Определение зависимости модуля сопротивления контура от частоты z(w), y(w).
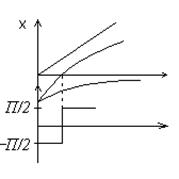
2) Определение j(w)
3) Определение возможных видов резонансов и резонансных частот. Резонансом в электрической цепи называется явление совпадение по фазе напряжения и тока на входе цепи, при этом входное сопротивление цепи чисто активное. Мощность. Потребляемая из цепи – активная. Рез=>j=0=>S=P.
I. Последовательный резонансный контур. Резонанс напряжений.
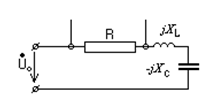
- простейший контур, в котором резонанс.
Z =R+j(XL-XC) Уравнение резонанса 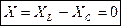
XL0=XC0 (для этой цепи) w0L=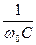 ;
; 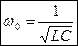
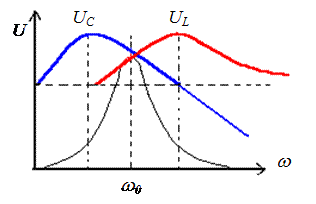
Добротность последовательного колебательного контура – величина, которая показывает во сколько раз напряжение на индуктивности или емкости при резонансе больше входного напряжения.
q=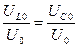 ;
; 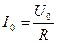 ; UL0=I0w0L; UC0=I0
; UL0=I0w0L; UC0=I0 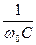
q= ; q=
; q= ; q=
; q=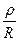 ;
; 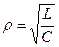 - волновое сопротивление.
- волновое сопротивление.
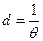 - затухание контура.
- затухание контура. 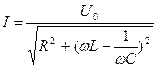 ;
;
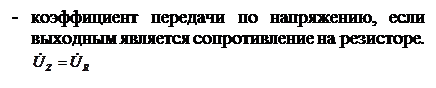 KU(jw)=
KU(jw)=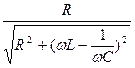
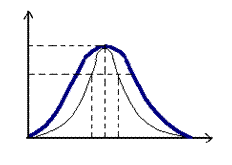
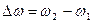
- полоса пропускания.
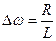
Вне полосы пропускания частот, мощность (активная) сигнала по сравнению с max, уменьшается в 2 раза.
P(w1)=P(w2)=1/2 Pmax q1>q2; q= - чем выше q, тем острее пик.
- чем выше q, тем острее пик.
WM (энергия магнитного поля) = 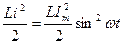
WЭ (энергия электрического поля) = 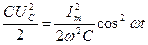
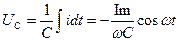 W=WM + WЭ=WMmax=WЭ max
W=WM + WЭ=WMmax=WЭ max
При резонансе обмен энергией происходит между индуктивностью и конденсатором. Из сети потребляется активная мощность, рассеиваемая на активном сопротивлении цепи (2 реактивных элемента обмениваются енергией т.е. колеблются).
 J 1) R=0
J 1) R=0 (контур идеальный)
XL=wL XC= X= XL- XC
X= XL- XC 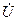 L0
L0 
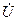 R
R 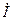 1
1 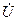 C0
C0 2) R ¹ 0

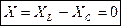
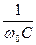 ;
; 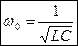
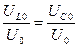 ;
; 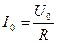 ; UL0=I0w0L; UC0=I0
; UL0=I0w0L; UC0=I0 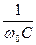
 ; q=
; q= ; q=
; q=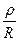 ;
; 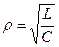 - волновое сопротивление.
- волновое сопротивление.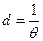 - затухание контура.
- затухание контура. 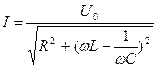 ;
;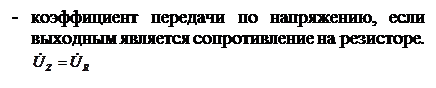 KU(jw)=
KU(jw)=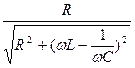

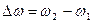
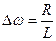
 - чем выше q, тем острее пик.
- чем выше q, тем острее пик.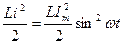
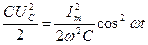
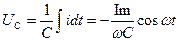 W=WM + WЭ=WMmax=WЭ max
W=WM + WЭ=WMmax=WЭ max J 1) R=0 (контур идеальный) XL=wL XC=
J 1) R=0 (контур идеальный) XL=wL XC=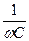 X= XL- XC
X= XL- XC 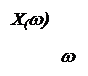
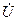 L0
L0 
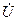 R
R 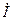 1
1 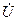 C0
C0 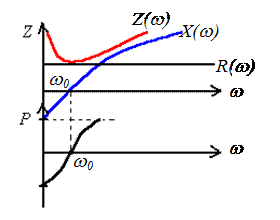
 2014-02-02
2014-02-02 869
869