Резюме
Цели
Указания по самостоятельному изучению темы
ГЛАВА 5. Модели долгосрочного страхования жизни
Иметь представление:
· о видах долгосрочного страхования жизни;
· о принципах назначения разовых нетто-премий для основных непрерывных и дискретных видов страхования.
Знать:
· теорему о дисперсии приведенной ценности;
· основные вычислительные формулы для расчета нетто-премий.
Уметь:
· вычислять актуарную стоимость будущей страховой выплаты;
· вычислять разовые нетто-премии для различных видов страхования жизни.
Долгосрочное страхование характеризуется тем, что при расчетах принимается во внимание изменение ценности денег с течением времени.
Поэтому теория долгосрочного страхования существенно опирается на теорию сложных процентов. Мы будем предполагать, что интенсивность процентов 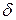 не меняется с течением времени,
не меняется с течением времени, 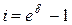 , будет обозначать эффективную годовую процентную ставку,
, будет обозначать эффективную годовую процентную ставку, 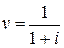 – коэффициент дисконтирования.
– коэффициент дисконтирования.
Страховое возмещение обычно выплачивается в виде одиночной суммы в момент смерти застрахованного – такие виды страхования часто называют непрерывными. Однако возможны выплаты и в другие моменты времени. Наиболее важен случай, когда выплата производится не в момент смерти, а в следующий за ним день рождения застрахованного – такие виды страхования часто называют дискретными. Если считать, что возраст застрахованного в момент заключения договора – целое число, то дискретные договора можно описать как договоры с выплатой страховой суммы в очередную, после момента смерти, годовщину заключения договора. В самом общем случае момент выплаты страховой суммы является некоторой функцией 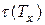 от остаточного времени жизни застрахованного.
от остаточного времени жизни застрахованного.
Величина страхового возмещения, как правило, фиксирована и мы будем принимать ее в качестве единицы измерения денежных сумм. Однако в ряде случаев возмещение может увеличиваться или уменьшаться в зависимости от момента выплаты. С этой целью мы введем функцию  , которая определяет величину страховой выплаты в случае смерти в момент
, которая определяет величину страховой выплаты в случае смерти в момент 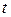 .
.
Две функции 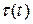 и
и  , определяют общую модель страхования жизни. С ее помощью можно единообразно описать различные конкретные виды страхования.
, определяют общую модель страхования жизни. С ее помощью можно единообразно описать различные конкретные виды страхования.
Пожизненное страхование.
Простейшим видом долгосрочного страхования является пожизненное страхование. При этом виде страхования фиксированная страховая сумма 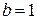 выплачивается в момент смерти и поэтому
выплачивается в момент смерти и поэтому
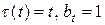 .
.
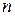 - летнее чисто накопительное страхование
- летнее чисто накопительное страхование
При этом виде страхования выплата страховой суммы фиксированной величины 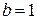 производится в момент
производится в момент 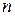 , если застрахованный дожил до этого момента. В случае смерти до момента
, если застрахованный дожил до этого момента. В случае смерти до момента 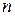 компания не платит ничего. Этот вид страхования описывается следующими функциями
компания не платит ничего. Этот вид страхования описывается следующими функциями 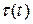 и
и 
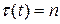 ,
, 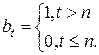
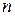 - летнее временное страхование жизни.
- летнее временное страхование жизни.
При этом виде страхования выплата фиксированной страховой суммы 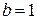 производится в момент смерти, если застрахованный умер в течение срока действия договора, т.е.на протяжении
производится в момент смерти, если застрахованный умер в течение срока действия договора, т.е.на протяжении 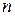 лет с момента заключения договора. Если же застрахованный прожил эти
лет с момента заключения договора. Если же застрахованный прожил эти 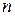 лет, то компания не платит ничего. Этот вид страхования можно описать функциями:
лет, то компания не платит ничего. Этот вид страхования можно описать функциями:
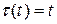 ,
, 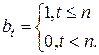
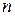 - летнее смешанное страхование
- летнее смешанное страхование
При этом виде страхования выплата фиксированной страховой суммы 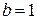 производится на следующих условиях. Если смерть застрахованного наступит до истечения срока действия договора, то страховая сумма выплачивается в момент смерти. Если же застрахованный дожил до окончания срока действия договора, то страховая сумма выплачивается в момент
производится на следующих условиях. Если смерть застрахованного наступит до истечения срока действия договора, то страховая сумма выплачивается в момент смерти. Если же застрахованный дожил до окончания срока действия договора, то страховая сумма выплачивается в момент 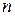 окончания срока действия договора. Нетрудно понять, что этот вид страхования выполняет функции как собственно страхования, так и накопления средств. Этот вид страхования описывается следующими функциями
окончания срока действия договора. Нетрудно понять, что этот вид страхования выполняет функции как собственно страхования, так и накопления средств. Этот вид страхования описывается следующими функциями 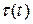 и
и  :
:
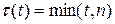 ,
, 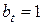 .
.
Пожизненное страхование, отсроченное на 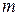 лет
лет
При этом виде страхования выплата фиксированной страховой суммы 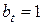 производится в момент смерти застрахованного, но только если она произошла по истечении
производится в момент смерти застрахованного, но только если она произошла по истечении 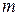 -летнего срока с момента заключения договора. Если застрахованный умрет раньше, чем через
-летнего срока с момента заключения договора. Если застрахованный умрет раньше, чем через 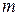 лет после заключения договора, страховое возмещение не выплачивается вовсе.
лет после заключения договора, страховое возмещение не выплачивается вовсе.
Этот вид страхования описывается следующими функциями 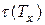 и
и  :
:
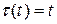 ,
, 
Страхование с переменной страховой выплатой
Во всех рассмотренных выше примерах величина страховой выплаты была фиксирована и не зависела от момента выплаты. Существуют виды страхования, когда страховое возмещение может меняться. В качестве примера рассмотрим простейший случай – пожизненное страхование с непрерывно увеличивающимся страховым возмещением. При этом виде страхования компания выплачивает в момент смерти сумму, равную  . Этот случай описывается общей моделью при
. Этот случай описывается общей моделью при
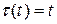 ,
, 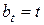 .
.
Теорема о дисперсии приведенной ценности
Рассмотрим некоторый договор страхования, описываемый с помощью функций 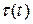 и
и  . Пусть
. Пусть
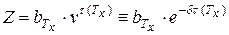
приведенная стоимость страхового пособия на момент заключения договора с человеком в возрасте 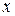 лет. Чтобы подчеркнуть зависимость случайной величины
лет. Чтобы подчеркнуть зависимость случайной величины 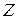 от процентной ставки, будем писать
от процентной ставки, будем писать  . Обозначим также через
. Обозначим также через
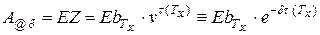
актуарную приведенную стоимость будущей страховой выплаты, если интенсивность процентов равна 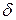 .
.
Предположим теперь, что в нашей общей модели страхования функция
 принимает только значения 0 и 1, т.е. если в соответствии с условиями договора в некоторый момент
принимает только значения 0 и 1, т.е. если в соответствии с условиями договора в некоторый момент 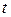 выплачивается страховое возмещение, то его величина не зависит от момента выплаты. Все описанные выше виды страхования, кроме страхования с переменной страховой выплатой, удовлетворяют этому условию. Тогда
выплачивается страховое возмещение, то его величина не зависит от момента выплаты. Все описанные выше виды страхования, кроме страхования с переменной страховой выплатой, удовлетворяют этому условию. Тогда 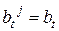 и поэтому
и поэтому
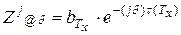 ,
,
т.е. 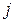 -я степень современной величины будущей страховой выплаты, подсчитанной для интенсивности процентов
-я степень современной величины будущей страховой выплаты, подсчитанной для интенсивности процентов 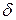 , совпадает с современной величиной будущей страховой выплаты, но подсчитанной для интенсивности процентов
, совпадает с современной величиной будущей страховой выплаты, но подсчитанной для интенсивности процентов 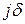 . Тем более равенство верно для средних значений, т.е.
. Тем более равенство верно для средних значений, т.е.
 .
.
В частности,
 .
.
Разовые нетто-премии для основных непрерывных видов страхования
Как следует из изложенного выше, разовая нетто-премия для любого договора страхования, описываемого функциями  и
и 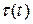 , есть
, есть
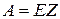 ,
,
где 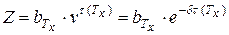 – величина страхового возмещения, приведенная на момент заключения договора, а
– величина страхового возмещения, приведенная на момент заключения договора, а 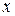 – возраст застрахованного в этот момент.
– возраст застрахованного в этот момент.
Для конкретных видов страхования общая формула может быть упрощена и конкретизирована. Для того, чтобы подчеркнуть, что речь идет о конкретных видах страхования, переменные 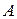 и
и 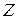 снабжаются различными индексами. Основные правила, регулирующие индексы, следующие:
снабжаются различными индексами. Основные правила, регулирующие индексы, следующие:
1. Справа внизу во всех случаях ставится возраст застрахованного на момент заключения договора: 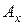 .
.
2. Если договор страхования непрерывный, т.е. страховое пособие выплачивается в момент смерти, то сверху ставится черта: 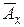 .
.
3. Если договор действует ограниченный период времени 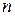 , то после возраста
, то после возраста 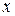 через двоеточие ставится дополнительный индекс
через двоеточие ставится дополнительный индекс 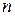 , обрамленный уголком:
, обрамленный уголком: 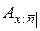 .
.
4. Если договор отсрочен на 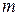 лет, то внизу слева ставится индекс
лет, то внизу слева ставится индекс  :
: 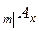 .
.
5. Если величина страховой суммы регулярно возрастает, то добавляется буква 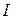 :
: 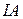 .
.
Рассмотрим теперь конкретные договоры страхования.
Пожизненное страхование
Современная стоимость страховой выплаты в момент заключения договора с человеком в возрасте 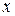 лет обозначается
лет обозначается 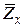 , а актуарная современная стоимость страховой суммы в момент заключения договора
, а актуарная современная стоимость страховой суммы в момент заключения договора 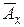 .
.
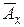 можно следующим образом выразить через характеристики времени жизни:
можно следующим образом выразить через характеристики времени жизни:
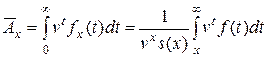 .
.
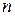 - летнее чисто накопительное страхование.
- летнее чисто накопительное страхование.
Актуарная приведенная стоимость страховой суммы обозначается 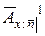 и дается формулой:
и дается формулой:
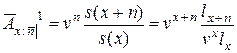 .
.
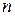 - летнее смешанное страхование
- летнее смешанное страхование
Актуарная современная стоимость страховой суммы в момент заключения договора с человеком в возрасте 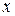 лет вычисляется по формуле:
лет вычисляется по формуле:
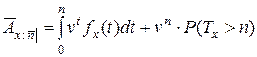 .
.
Пожизненное страхование, отсроченное на 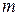 лет
лет
Для данного вида страхования актуарная современная стоимость вычисляется по формуле:
 .
.
Страхование с переменной страховой выплатой.
Актуарная современная стоимость страховой суммы обозначается 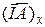 и вычисляется:
и вычисляется:
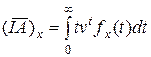 .
.
Долгосрочное страхование характеризуется тем, что при расчетах принимается во внимание изменение ценности денег с течением времени.
Поэтому теория долгосрочного страхования существенно опирается на теорию сложных процентов. Интенсивность процентов 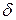 не меняется с течением времени,
не меняется с течением времени, 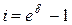 – эффективная годовая процентная ставка,
– эффективная годовая процентная ставка, 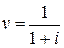 – коэффициент дисконтирования.
– коэффициент дисконтирования.
Страховое возмещение обычно выплачивается в виде одиночной суммы в момент смерти застрахованного – такие виды страхования часто называют непрерывными. Однако возможны выплаты и в другие моменты времени. Наиболее важен случай, когда выплата производится не в момент смерти, а в следующий за ним день рождения застрахованного – такие виды страхования часто называют дискретными. Если считать, что возраст застрахованного в момент заключения договора – целое число, то дискретные договора можно описать как договоры с выплатой страховой суммы в очередную, после момента смерти, годовщину заключения договора. В самом общем случае момент выплаты страховой суммы является некоторой функцией 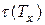 от остаточного времени жизни застрахованного.
от остаточного времени жизни застрахованного.
Величина страхового возмещения, как правило, фиксирована и мы будем принимать ее в качестве единицы измерения денежных сумм. Однако в ряде случаев возмещение может увеличиваться или уменьшаться в зависимости от момента выплаты. С этой целью мы введем функцию  , которая определяет величину страховой выплаты в случае смерти в момент
, которая определяет величину страховой выплаты в случае смерти в момент 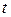 .
.
Две функции 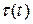 и
и  , определяют общую модель страхования жизни. С ее помощью можно единообразно описать различные конкретные виды страхования.
, определяют общую модель страхования жизни. С ее помощью можно единообразно описать различные конкретные виды страхования.
1. В чем отличие долгосрочного страхования от краткосрочного?
2. Перечислите основные виды долгосрочного страхования жизни. В чем они заключаются?
3. Сформулируйте теорему о дисперсии приведенной ценности.
4. Что называют актуарной приведенной стоимостью (ценностью)?
5. Принципы назначения разовых нетто-премий для основных непрерывных видов долгосрочного страхования.
 2014-02-02
2014-02-02 605
605








