Понятие частного коэффициента корреляции

Частные коэффициенты корреляции характеризуют связи двух признаков из совокупности признаков при условии, что все связи этих признаков с другими признаками элиминированы, т.е. закреплены на условно-постоянном (среднем) уровне.

Таким образом, существуют парный (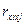), частный (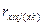)и множественный коэффициент корреляции ().

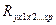Введем обозначение 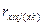- коэффициент частной линейной корреляции, характеризующий степень линейной зависимости между признаками х_i и x_j при исключенном влиянии третьей величины x_k, включенной в модель.

Если парный коэффициент корреляции между двумя случайными величинами оказался больше частного коэффициента между теми же случайными величинами, то это говорит о том, что третья фиксированная величина усиливает взаимосвязь между изучаемыми величинами, т.е. более высокое значение парного коэффициента обусловлено присутствием третьей величины.

Более низкое значение парного коэффициента корреляции в сравнении с соответствующим частным коэффициентом корреляции свидетельствует об ослаблении связи между изучаемыми величинами действием фиксируемой величины.

Частные коэффициенты корреляции для двухфакторной линейной модели можно рассчитать с помощью парных коэффициентов корреляции:

.

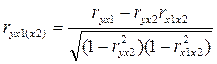Частный коэффициент корреляции изменяется в пределах от -1 до +1. Если частный коэффициент корреляции равен 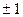, то связь между двумя величинами функциональная, а равенство нулю свидетельствует о линейной независимости этих величин.