Лекция № 11.
Амплитудной модуляцией (АМ) называется процесс изменения амплитуды несущего колебания 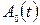 под воздействием модулирующего сигнала
под воздействием модулирующего сигнала 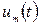 . В результате амплитуда несущей получает приращение
. В результате амплитуда несущей получает приращение  и становится равной
и становится равной 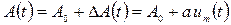 ,
,
где 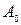 – амплитуда несущей;
– амплитуда несущей; 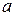 – коэффициент пропорциональности, выбираемый так, чтобы амплитуда
– коэффициент пропорциональности, выбираемый так, чтобы амплитуда 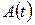 всегда была положительной. Частота и фаза несущего гармонического колебания при АМ остаются неизменными.
всегда была положительной. Частота и фаза несущего гармонического колебания при АМ остаются неизменными.

На рисунке показано, что в соответствии с мгновенными значениями 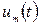 амплитуда несущей
амплитуда несущей 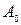 увеличивается до значения
увеличивается до значения 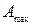 получая приращение
получая приращение 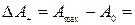
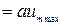 , то уменьшается до
, то уменьшается до  , получая приращение
, получая приращение 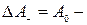 .
.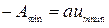 При этом амплитуда
При этом амплитуда 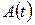 повторяет форму модулирующего сигнала
повторяет форму модулирующего сигнала 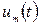 . В АМ сигнале амплитуда
. В АМ сигнале амплитуда 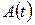 является огибающей высокочастотного заполнения
является огибающей высокочастотного заполнения  , которая на рисунке изображена штриховой линией.
, которая на рисунке изображена штриховой линией.
Для математического описания АМ сигнала вместо коэффициента пропорциональности 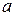 , зависящего от конкретной схемы модулятора, вводится коэффициент модуляции
, зависящего от конкретной схемы модулятора, вводится коэффициент модуляции 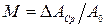 , который физически означает относительное значение приращения. Здесь
, который физически означает относительное значение приращения. Здесь 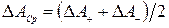 – среднее арифметическое значение приращения амплитуды. Поскольку среднее значение амплитуды АМ сигнала во время модуляции
– среднее арифметическое значение приращения амплитуды. Поскольку среднее значение амплитуды АМ сигнала во время модуляции  , то коэффициент модуляции численно равен
, то коэффициент модуляции численно равен
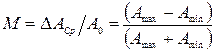 .
.
Коэффициент модуляции – это отношение разности между максимальным и минимальным значениями амплитуд АМ сигнала к сумме этих значений. Часто коэффициент модуляции выражается в процентах 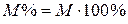 . Однако при всех расчетах АМ сигналов обычно пользуются коэффициентом модуляции
. Однако при всех расчетах АМ сигналов обычно пользуются коэффициентом модуляции 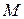 не в процентах, а в относительных единицах.
не в процентах, а в относительных единицах.
Для симметричного модулирующего сигнала 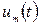 АМ сигнал также будет симметричным:
АМ сигнал также будет симметричным: 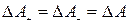 и
и
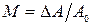 ,
,
то есть коэффициент модуляции равен отношению максимального приращения амплитуды к амплитуде несущей. Физически 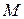 характеризует собой глубину амплитудной модуляции и может изменяться в пределах
характеризует собой глубину амплитудной модуляции и может изменяться в пределах 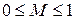 .
.
Аналитическое выражение (математическая модель) любого АМ сигнала, с учетом коэффициента модуляции, будет выглядеть следующим образом:
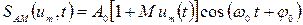 .
.
Амплитудная модуляция гармоническим колебанием.
В простейшем случае модулирующий сигнал 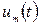 является гармоническим колебанием с частотой
является гармоническим колебанием с частотой 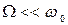 и начальной фазой
и начальной фазой 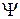 . При этом аналитическое выражение однотонального АМ сигнала будет выглядеть следующим образом:
. При этом аналитическое выражение однотонального АМ сигнала будет выглядеть следующим образом:
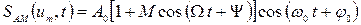
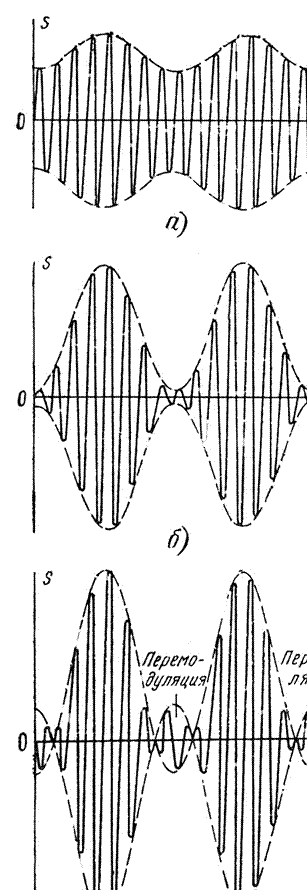
На рисунке показаны временные диаграммы однотонального АМ сигнала при различных значениях коэффициента модуляции 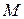 .
.
Характерное искажение сигнала возникает при перемодуляции, когда форма огибающей перестает повторять форму модулирующего гармонического колебания.
В однотональном АМ сигнале имеется три гармонических спектральных составляющих с частотами: 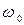 – несущей;
– несущей; 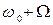 – верхней боковой;
– верхней боковой; 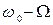 – нижней боковой.
– нижней боковой.
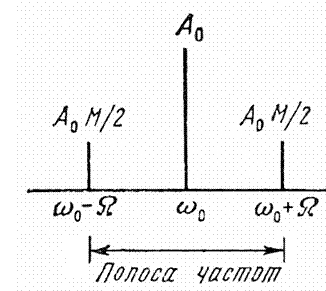
Спектральная диаграмма однотонального АМ сигнала симметрична относительно несущей частоты 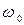 . Амплитуды боковых колебаний одинаковы и даже при
. Амплитуды боковых колебаний одинаковы и даже при 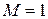 не превышают половины амплитуды несущего колебания.
не превышают половины амплитуды несущего колебания.
Амплитудная модуляция при сложном модулирующем сигнале.
Гармонические модулирующие сигналы и соответственно однотональный АМ сигнал на практике встречаются редко. В большинстве случаем модулирующие первичные сигналы 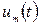 являются сложными функциями времени.
являются сложными функциями времени.
Спектр АМ сигнала при сложном модулирующем сигнале 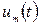 можно построить исходя из следующих рассуждений. Любой сложный сигнал
можно построить исходя из следующих рассуждений. Любой сложный сигнал 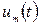 можно представить в виде суммы конечной (или бесконечной) гармонических составляющих, воспользовавшись рядом Фурье. Каждая гармоническая составляющая сигнала
можно представить в виде суммы конечной (или бесконечной) гармонических составляющих, воспользовавшись рядом Фурье. Каждая гармоническая составляющая сигнала 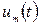 с частотой
с частотой 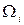 вызовет в АМ сигнале две боковые составляющие с частотами
вызовет в АМ сигнале две боковые составляющие с частотами 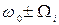 . Множество гармонических составляющих в модулирующем сигнале
. Множество гармонических составляющих в модулирующем сигнале 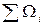 вызовет множество боковых составляющих с частотами
вызовет множество боковых составляющих с частотами 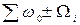 . Это показано на рисунке.
. Это показано на рисунке.
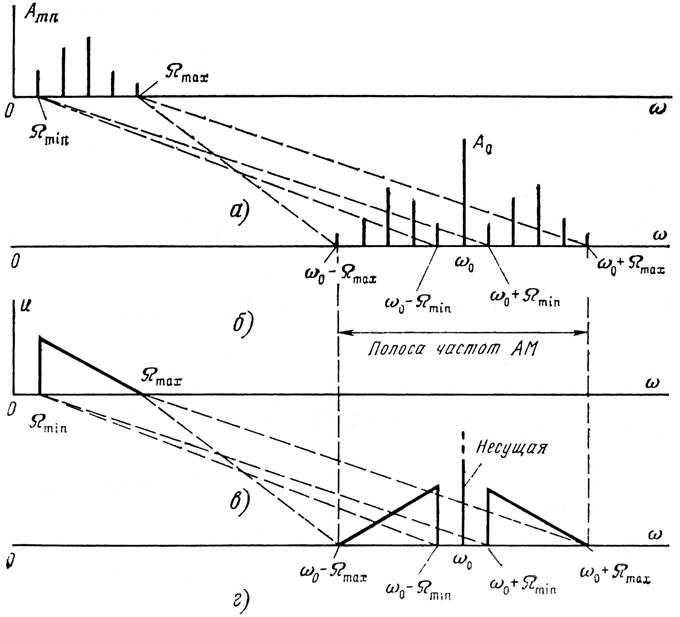
Спектральные диаграммы: а) – модулирующего многотонального сигнала; б) – АМ сигнала при многотональной модуляции; в) – модулирующего сигнала с непрерывным спектром; г) – АМ сигнала при модуляции сигнала непрерывным спектром.
В спектре сложномодулированного АМ сигнала, кроме несущего колебания с частотой 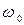 , содержатся группы верхних и нижних боковых колебаний, которые образуют верхнюю боковую и нижнюю боковую полосу АМ сигнала. При этом верхняя боковая полоса частот полностью повторяет спектральную диаграмму сигнала
, содержатся группы верхних и нижних боковых колебаний, которые образуют верхнюю боковую и нижнюю боковую полосу АМ сигнала. При этом верхняя боковая полоса частот полностью повторяет спектральную диаграмму сигнала 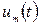 , сдвинутую в область высоких частот на величину
, сдвинутую в область высоких частот на величину 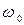 . Нижняя боковая полоса частот также повторяет спектральную диаграмму сигнала
. Нижняя боковая полоса частот также повторяет спектральную диаграмму сигнала 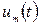 , но частоты в не располагаются в зеркальном (обратном) порядке относительно несущей частоты
, но частоты в не располагаются в зеркальном (обратном) порядке относительно несущей частоты 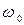 .
.
Из этого следует вывод: ширина спектра АМ сигнала  равна удвоенному значению наиболее высокой частоты
равна удвоенному значению наиболее высокой частоты 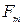 спектра модулирующего низкочастотного сигнала, то есть
спектра модулирующего низкочастотного сигнала, то есть
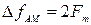
 2014-02-02
2014-02-02 13334
13334
