Типовые динамические звенья
Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.
Типовые динамические звенья подразделяются на:
1. безынерционное звено (усилительное);
4. идеальное дифференцирующее звено;
5. реальное дифференцирующее звено;
6. идеальное интегрирующее звено;
7. реальное интегрирующее звено;
8. форсирующее звено;
9. звено чистого запаздывания.
Безынерционное звено является простейшим среди всех типовых звеньев. Оно передает сигнал со входа на выход мгновенно, без искажений его формы. В звене может происходить только усиление или ослабление мгновенных значений входной величины.
Связь между мгновенными значениями входной величины x(t) и выходной величины y(t) описывается алгебраическим уравнением

Передаточные свойства звена определяются лишь одним параметром – передаточным коэффициентом k.
При единичном ступенчатом воздействии x(t)= 1 (t), приложенном в момент t =0, выходная величина мгновенно изменяется и принимает значение k (рис.а).
1. Переходная характеристика звена имеет вид
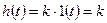
2. Импульсная переходная характеристика (функция веса) (рис.б)
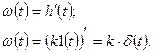
3. Уравнение звена в операционной форме
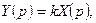
отсюда передаточная функция
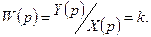
4. Амплитудно-фазовая характеристика (АФХ) звена описывается функцией
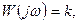
которой на комплексной плоскости соответствует одна точка на действительной оси (рис.е).
5. Амплитудно-частотная характеристика (АЧХ)
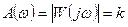
представляет собой прямую, параллельную оси частот (рис.в).
Это означает, что сигналы любой частоты (от нуля до бесконечности) проходят через безынерционное звено с одинаковым отношением амплитуд выходной и входной величин, равным k.
6. Выражение для фазовой частотной характеристики (ФЧХ) (рис.г)
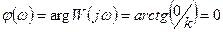
показывает, что безынерционное звено не создает фазовых сдвигов между входной и выходной величиной. Это и оправдывает название звена.
7. Логарифмическая амплитудная частотная характеристика (ЛАЧХ) безынерционного звена
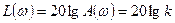
так же, как и его АЧХ, является прямой линией, параллельной оси абсцисс (рис.д).
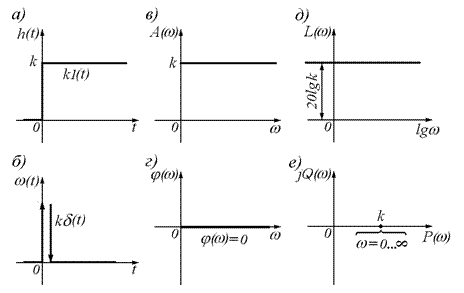 |
Графики соответствующих характеристик изображены на рис.:
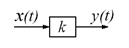 На алгоритмических схемах безынерционное звено изображают в виде прямоугольника, внутри которого указывают буквенное обозначение или числовое значение передаточного коэффициента k (см. рис.).
На алгоритмических схемах безынерционное звено изображают в виде прямоугольника, внутри которого указывают буквенное обозначение или числовое значение передаточного коэффициента k (см. рис.).
Пример:
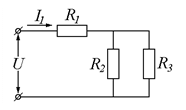
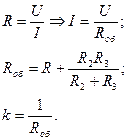
Здесь U - входная характеристика;
I - выходная характеристика.
Примерами могут также служить любая электрическая цепь, состоящая из сопротивлений и являющаяся усилительным звеном; рычаги и зубчатые передачи. В практике усилительные звенья встречаются очень редко.
 2014-02-02
2014-02-02 5890
5890








