2014-02-02
12624
Анализ выражений для токов через p-n переход при прямых и обратных напряжениях позволяет установить аналитическую зависимость:
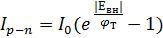
Это уравнение называется уравнением диода или уравнением Шокли, где I0 – тепловой ток или обратный ток насыщения.
Термин «тепловой» отражает сильную температурную зависимость I0 от температуры, а также тот факт, что I0 = 0 при Т = 0 К.
Термин «обратный ток насыщения» отражает тот факт, что при отрицательном напряжении Евн и |Евн|>>φт, обратный ток идеализированного диода равен (-I0) и не зависит от Евн.
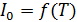
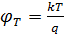, где k = 1,38*
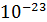Дж/К – постоянная Больцмана;
q = 1,6*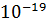
Кл;
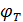=26 БмВ при Т = 300 К.
Действительно,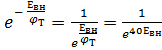 
близко к нулю.
Это значит, что при обратном включении Ip-n(обр) = -I0 и не зависит от величины обратного напряжения.
Вольт-амперная характеристика(ВАХ)
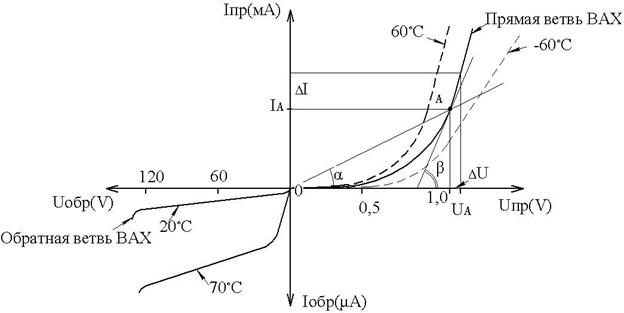p-n перехода
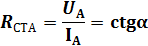
Статическое сопротивление p-n перехода в рабочей точке (А) определяется как отношение напряжения в этой точке к току, соответствующему этому напряжению или равно ctgα – угла образованного прямой, проходящей через начало координат и рабочую точку(А) и осью абсцисс(Х).
Дифференциальное сопротивление p-n перехода в рабочей точке(А) определяется как отношение приращения напряжения в этой точке к приращению тока, соответствующего этому приращению напряжения
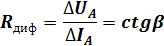
или равно ctgβ – угла образованного касательной к этой точке и осью абсцисс.
Реальная ветвь(прямая) ВАХ перехода отклоняется от идеальной ВАХ в основном за счёт падения напряжения на сопротивлении базы(rБ), с учётом этого уравнение перехода может быть определено:
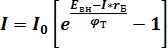
Прологарифмировав это выражение можно определить падение напряжения на переходе при прямом включении.
Заменив Eвн на Uпр, получим:
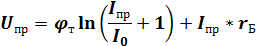
Для малых токов Iпр имеем:
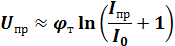
Статическое и дифференциальное сопротивление для обратной ветви ВАХ рассчитывается аналогично прямой ветви ВАХ
Rст.пр << Rст.обр.;
Rдиф.пр << Rдиф.обр.; при Uпр.= |Uобр.|>U, |Uобр.|<Uпроб.
