Частные производные. Касательная плоскость и нормаль
Пусть задана функция 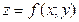 . Так как х и у – независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение
. Так как х и у – независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение 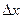 , сохраняя значение
, сохраняя значение
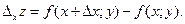
Аналогично получаем частное приращение z по у:
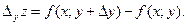
Полное приращение 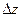 функции
функции 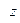 определяется равенством
определяется равенством
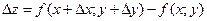 .
.
Если существует предел
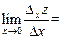
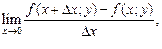
то он называется частной производной функции 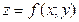 в точке
в точке 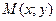 по переменной х и обозначается одним из символов:
по переменной х и обозначается одним из символов:
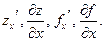
Частные производные по х в точке 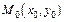 обычно обозначают символами
обычно обозначают символами 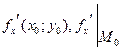 .
.
Аналогично определяется и обозначается частная производная от 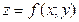 по переменной у.
по переменной у.
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции  находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).
находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).
|
|
|
Пример 2. Найти частные производные функции 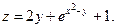
Решение.
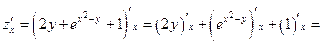
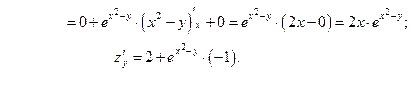
Графиком функции 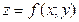 является некоторая поверхность.
является некоторая поверхность.
График функции 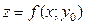 есть линия пересечения этой поверхности с плоскостью
есть линия пересечения этой поверхности с плоскостью 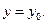 Исходя из геометрического смысла производной для функции одной переменной заключаем, что
Исходя из геометрического смысла производной для функции одной переменной заключаем, что 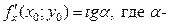 угол между осью 0х и касательной, проведенной к кривой
угол между осью 0х и касательной, проведенной к кривой 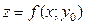 в точке
в точке  (рис. 3). Аналогично
(рис. 3). Аналогично 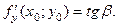
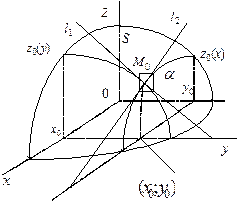

Рис. 3 Рис. 4
Рассмотрим одно из геометрических приложений частных производных функции двух переменных. Пусть функция 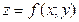 дифференцируема в точке
дифференцируема в точке 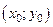 некоторой области
некоторой области 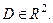 Рассечем поверхность, изображающую функцию z, плоскостями
Рассечем поверхность, изображающую функцию z, плоскостями 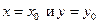 (рис. 4). Плоскость
(рис. 4). Плоскость 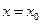 пересекает поверхность S по некоторой линии
пересекает поверхность S по некоторой линии 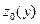 , уравнение которой получается подстановкой в выражение исходной функции
, уравнение которой получается подстановкой в выражение исходной функции 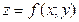 вместо
вместо 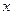 числа
числа 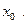 Точка
Точка  принадлежит кривой
принадлежит кривой 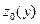 . В силу дифференцируемости функции z в точке М0 функция
. В силу дифференцируемости функции z в точке М0 функция 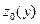 также является дифференцируемой в точке
также является дифференцируемой в точке 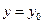 . Следовательно, в этой точке в плоскости
. Следовательно, в этой точке в плоскости 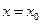 к кривой
к кривой 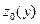 может быть проведена касательная
может быть проведена касательная  .
.
Проводя аналогичные рассуждения для сечения 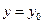 , построим касательную
, построим касательную 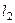 к кривой
к кривой 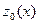 в точке
в точке 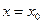 . Прямые
. Прямые 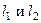 определяют плоскость
определяют плоскость 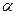 , которая называется касательной плоскостью поверхности S в точке М0.
, которая называется касательной плоскостью поверхности S в точке М0.
Составим её уравнение. Так как плоскость проходит через точку 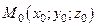 , то её уравнение может быть записано в виде
, то её уравнение может быть записано в виде
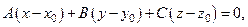
которое можно переписать так:
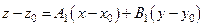 , (1)
, (1)
(разделив уравнение на –С и обозначив 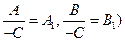 .
.
Найдем 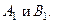
Уравнения касательных 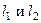 имеют вид
имеют вид
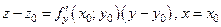 ,
,
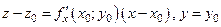
соответственно.
Касательная  лежит в плоскости
лежит в плоскости 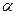 , следовательно, координаты всех точек
, следовательно, координаты всех точек  удовлетворяют уравнению (1). Этот факт можно записать в виде системы
удовлетворяют уравнению (1). Этот факт можно записать в виде системы
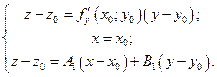
Разрешая эту систему относительно 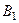 , получим, что
, получим, что 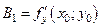 .
.
Проводя аналогичные рассуждения для касательной 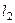 , легко установить, что
, легко установить, что 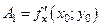 .
.
|
|
|
Подставив значения 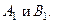 в уравнение (1), получаем исходное уравнение касательной плоскости:
в уравнение (1), получаем исходное уравнение касательной плоскости:
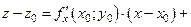

Прямая, проходящая через точку М0 и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется её нормалью.
Используя условие перпендикулярности прямой и плоскости легко получить канонические уравнения нормали:
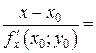

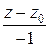 .
.
Замечание. Формулы касательной плоскости и нормали к поверхности получены для обыкновенных, т. е. не особых, точек поверхности. Точка М0 поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы не рассматриваем.
Пример 3. Написать уравнение касательной плоскости и нормали к параболоиду вращения 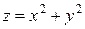 в точке
в точке 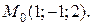
Решение: Здесь 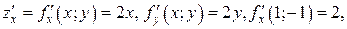
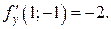 Пользуясь приведенными выше формулами, получаем уравнение касательной плоскости:
Пользуясь приведенными выше формулами, получаем уравнение касательной плоскости: 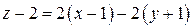 или
или
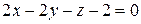 и уравнение нормали:
и уравнение нормали:
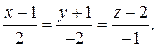
 2014-02-02
2014-02-02 1129
1129