Рассмотрим процесс всасывания одноцилиндрового приводного насоса одинарного действия, который откачивает жидкость из приемного резервуара открытого типа. Давление на поверхности жидкости постоянно и равно р о, ось цилиндра насоса, расположенного горизонтально, находится на высоте z в от свободной поверхности перекачиваемой жидкости плотностью ρ.
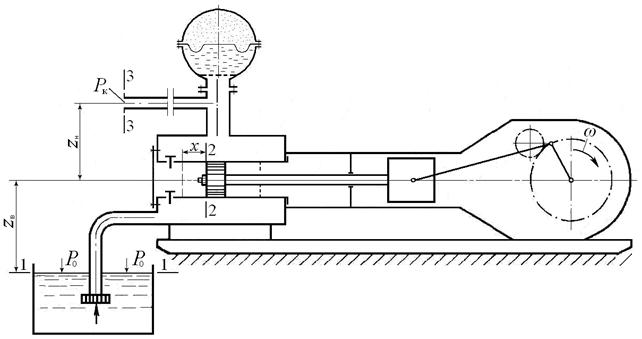
Рис. 10. Схема одноцилиндрового насоса одинарного действия.
Запишем уравнение Бернулли для двух сечений 1–1 и 2–2, приняв за плоскость сравнения сечение 1–1:

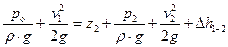 , (18)
, (18)
где v 1 – скорость перемещения поверхности жидкости в сечении 1–1; z 2= z в – вертикальное расстояние между сечением 1–1 и центром тяжести сечения 2–2, совпадающего с поверхностью поршня, контактирующего с жидкостью; p 2= p ц – давление жидкости в цилиндре насоса в период всасывания; v 2= v п – скорость движения жидкости в цилиндре, равная скорости поршня; 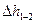 – потери энергии на перемещение жидкости между рассматриваемыми сечениями.
– потери энергии на перемещение жидкости между рассматриваемыми сечениями.
При круговой циркуляции жидкости (характерной для ряда операций, выполняемых на скважинах) поверхность жидкости в приемном резервуаре практически неподвижна и v 1=0.
Решая уравнение (18) относительно напора в цилиндре 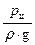 с учетом высказанных замечаний, получим:
с учетом высказанных замечаний, получим:
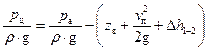 . (19)
. (19)
Потери энергии 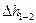 между сечениями 1-1 и 2-2 состоят из потерь в местных сопротивлениях
между сечениями 1-1 и 2-2 состоят из потерь в местных сопротивлениях 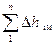 всасывающего трубопровода, потерь по длине
всасывающего трубопровода, потерь по длине 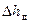 и потерь на преодоление сил инерции в цилиндре
и потерь на преодоление сил инерции в цилиндре 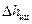 и в трубопроводе
и в трубопроводе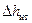 :
:
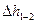 =
=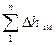 +
+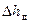 +
+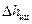 +
+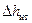 . (20)
. (20)
Установлено, что потери в клапане изменяются особым образом в сравнении с другими местными сопротивлениями, поэтому выделим эти потери в виде отдельного слагаемого. Тогда местные потери представим в виде:
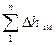 =
=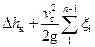 , (21)
, (21)
где 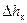 – потери напора во всасывающем клапане;
– потери напора во всасывающем клапане; 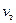 – скорость движения жидкости во всасывающем трубопроводе;
– скорость движения жидкости во всасывающем трубопроводе; 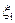 – коэффициент местных потерь i -го местного сопротивления всасывающего трубопровода.
– коэффициент местных потерь i -го местного сопротивления всасывающего трубопровода.
Выражая в уравнении (21) скорость движения жидкости в трубопроводе через скорость поршня, получим:
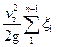 =
=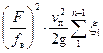 , (22)
, (22)
где 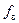 – площадь поперечного сечения всасывающего трубопровода.
– площадь поперечного сечения всасывающего трубопровода.
Потери напора по длине 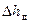 всасывающего трубопровода (в уравнении 20) представим по известной формуле Дарси-Вейсбаха:
всасывающего трубопровода (в уравнении 20) представим по известной формуле Дарси-Вейсбаха:
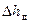 =
=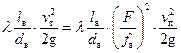 , (23)
, (23)
где λ – коэффициент гидравлического трения; l в – длина всасывающего трубопровода; d в – внутренний диаметр всасывающего трубопровода.
С учетом отмеченных замечаний и обозначений, уравнение (19) примет вид:
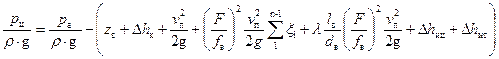 . (24)
. (24)
Объединим потери в местных сопротивлениях с потерями по длине:
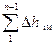 +
+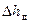 =
= 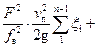
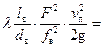
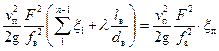 , (25)
, (25)
где 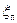 – приведенный коэффициент гидравлических сопротивлений всасывающего трубопровода.
– приведенный коэффициент гидравлических сопротивлений всасывающего трубопровода.
Подставив в уравнение (25) скорость движения поршня по уравнению (9), без учета влияния длины шатуна, получим:
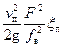
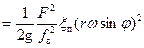 . (26)
. (26)
Потери напора на преодоление сил инерции жидкости в цилиндре вычислим по формуле:
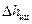
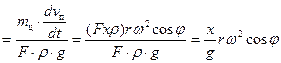 , (27)
, (27)
где m ц – масса жидкости в цилиндре.
Аналогично вычислим потери напора на преодоление сил инерции жидкости в трубопроводе:
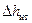
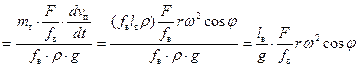 , (28)
, (28)
где m т – масса жидкости во всасывающем трубопроводе.
Для исключения из уравнений (26), (27) и (28) тригонометрических функций, воспользуемся уравнением (8) из которого выразим cos φ, а затем – sin φ:
cos φ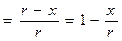 . (29)
. (29)
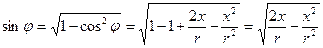 . (30)
. (30)
Подставив выражение (30) в уравнения (26), а (29)– в уравнения (27) и (28), получим:
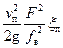 =
=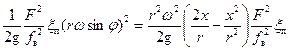 . (31)
. (31)
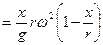 . (32)
. (32)
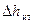
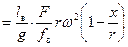 . (33)
. (33)
Кроме того, преобразуем в уравнении (24) выражение для скоростного напора к виду:
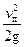
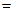
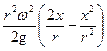 . (34)
. (34)
Подставив выражения (31) – (34) в уравнение (24) и выполнив некоторые преобразования, получим:
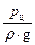
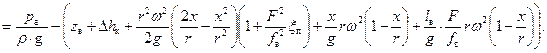 (35)
(35)
Умножив правую и левую части уравнения (35) на (ρ∙g) получим зависимость давления в цилиндре насоса от величины х перемещения поршня:
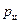
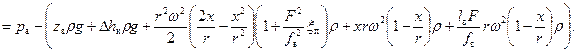 (36)
(36)
Анализ уравнения (36) показывает, минимальное давление в цилиндре насоса будет в начале процесса всасывания (при х =0), а максимальное – в конце (при х =2 r). Тогда, уравнение (36) соответственно примет вид:
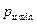
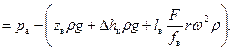 (37)
(37)
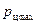
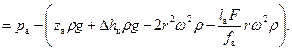 (38)
(38)
 2014-02-02
2014-02-02 1801
1801
