Дифференциального уравнения второго порядка методом прогонки

Пусть на отрезке 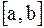требуется найти решение дифференциального уравнения:

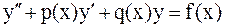, (1)

удовлетворяющее следующим краевым условиям:

;	(2) ;

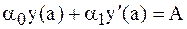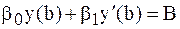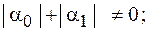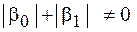Численное решение задачи состоит в нахождении приближенных значений 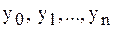искомого решения 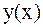в точках . Для этого разобьем отрезок 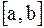на 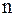равных частей с шагом 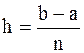. Полагая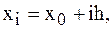 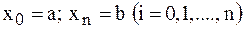и вводя обозначения 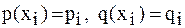, , 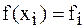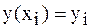для внутренних точек 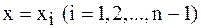отрезка 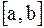, вместо дифференциального уравнения (1)–(2) получаем систему конечноразностных уравнений:

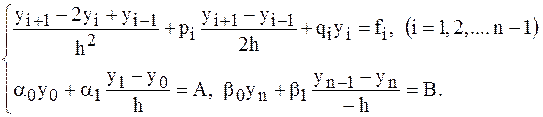
После соответствующих преобразований будем иметь

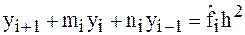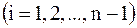, , (3)

где

.

Полученная система имеет 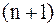линейных уравнений с 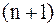неизвестными. Решим эту систему методом прогонки.

Решая уравнение (3) относительно 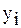, будем иметь

.

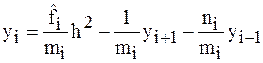Предположим, что из этого уравнения исключена неизвестная 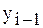. Тогда это уравнение примет вид

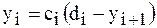, (4)

где 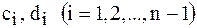– некоторые коэффициенты.

Отсюда 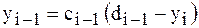. Подставляя это выражение в (3), получим 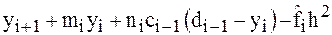и, следовательно,

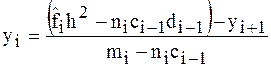. (5)

Сравнивая формулы (4) и (5), получим для определения 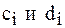рекуррентные формулы:

.

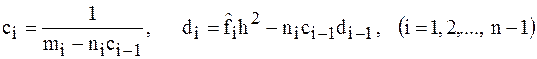Определим :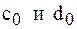

.

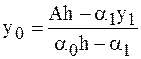Из формулы (4) при имеем

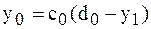. (6)

Поэтому

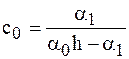, . (7)

На основании формул (6) и (7) последовательно определяются коэффициенты 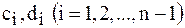до 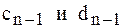включительно (прямой ход). Обратный ход начинается с определения 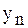. Решая систему

,

получим

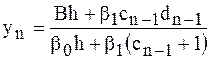
и по формуле (4) последовательно находим .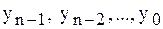

Для простейших краевых условий 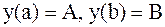формулы для 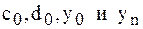упрощаются. Полагая 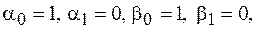получим .

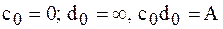Отсюда .

Пример. Методом прогонки решить краевую задачу:

.

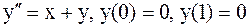Решение. Пусть .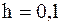

;

;

; ;

.

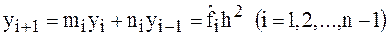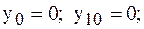
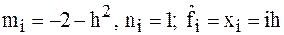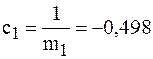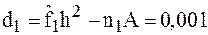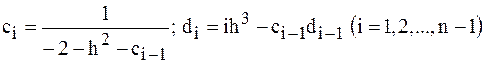Найденные значения 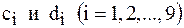записываем в первых двух строках таблицы. Используя известное значение 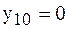, вычислим 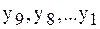и запишем в таблицу. Для значения в последней строке даны значения точного решения .

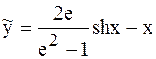Таблица 10

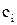		-0,498	-0,662	-0,878	-0,890	-0,900
		0,001	0,002	0,004	0,008	0,012
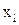		0,1	0,2	0,3	0,4	0,5
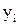		-0,025	-0,049	-0,072	-0,078	-0,081
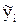		-0,015	-0,029	-0,041	-0,050	-0,057

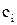	-0,908	-0,915	-0,921	-0,926
	0,16	0,022	0,028	0,035
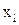	0,6	0,7	0,8	0,9
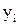	-0,078	-0,070	-0,055	-0,032
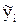	-0,058	-0,054	-0,044	-0,026