Лекция 6. Параметры цилиндрических зубчатых передач и колес

Параметры цилиндрических зубчатых передач и колес.

Зубчатое зацепление – кинематическая пара 4 класса, элементы которой представляют собой взаимоогибаемые кривые, передающие движение качением со скольжением.

Схема внешнего зубчатого зацепления представлена на рис. 16.

Рис.16

Основным кинематическим параметром зубчатой передачи является передаточное отношение

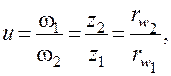
где 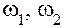– угловые скорости шестерни и колеса;

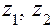– числа зубьев;

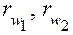– радиусы начальных окружностей

Начальные окружности это окружности, которые контактируют в полюсе зацепления и перекатываются друг по другу в процессе зацепления без скольжения.

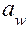– межосевое расстояние;

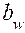– ширина зубчатого венца;

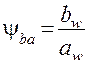– коэффициент ширины;

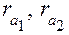– радиусы окружностей вершин зубьев;

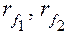– радиусы окружностей впадин зубьев.

Если провести, например на колесе, окружность произвольного радиуса 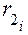, то расстояние между одноименными точками соседних зубьев, измеренное по этой окружности будет являться шагом зацепления P_i.

Длина окружности радиусом 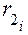вычисляется по формуле

,

,

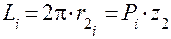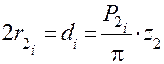обозначим ,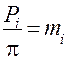

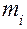– модуль зацепления, соответствующий шагу P_i, измеренному по окружности радиуса .

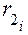Модуль зацепления является стандартным параметром зубчатой передачи, регламентированным ГОСТ 9563-60.

Окружность диаметром d, по которой измеряется шаг, соответствующий стандартному значению модуля, называется делительной.

ГОСТ 2185-66 регламентирует значения ,, .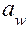

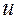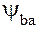Основной закон зацепления.

Рассмотрим передачу движения двумя взаимоогибаемыми кривыми (рис. 17).

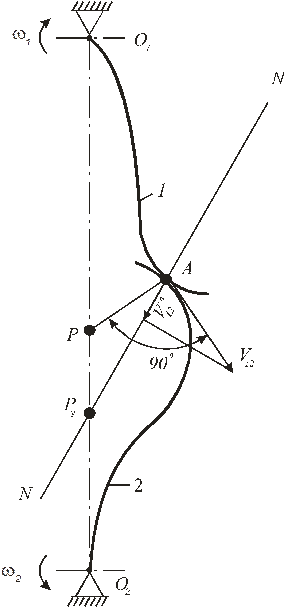NN – общая нормаль к звеньям 1,2 в точке их контакта А;

P – полюс зацепления (мгновенный центр относительного движения);

V₁₂ – скорость относительного движения;

V₁₂^п – проекция скорости V₁₂ на нормаль NN.

Если V₁₂^п ≠ 0, то звенья 1 и 2 будут либо внедряться друг в друга, либо расходиться, т.е. движение механизма будет невозможно.

Таким образом, движение с заданным передаточным отношением

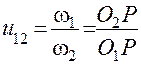
будет возможно только в том случае, если общая нормаль к сопрягаемым элементам кинематической пары будет

Рис. 17 проходить через полюс зацепления P.

Этот закон носит название теоремы Виллиса.

Основному закону зацепления удовлетворяют кривые, которые называются эвольвентами.