Общих способов построения математических моделей не существует. В каждом конкретном случае модель выбирается исходя из вида операции и ее целевой направленности, с учетом задач исследования (какие параметры требуется определить и влияние каких факторов отразить). Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой системы 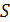 . Эта информация определяет основную цель моделирования системы
. Эта информация определяет основную цель моделирования системы 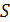 и позволяет сформулировать требования к разрабатываемой математической модели
и позволяет сформулировать требования к разрабатываемой математической модели 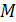 .
.
Математическую схемуможно определить как звено при переходе от содержательного (информационного) к математическому описанию процесса функционирования системы. Т.е., имеет место цепочка:
«Информационная модель – Математическая схема – Математическая модель».
При построении математической модели системы необходимо решить вопрос об ее полноте. Полнота модели регулируется в основном выбором границы «система 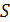 – внешняя среда
– внешняя среда 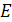 ».Также должна быть решена задача упрощения модели, которая помогает выделить основные свойства системы. Отнесение свойств системы к основным или второстепенным существенно зависит от цели моделирования системы.
».Также должна быть решена задача упрощения модели, которая помогает выделить основные свойства системы. Отнесение свойств системы к основным или второстепенным существенно зависит от цели моделирования системы.
Модель объекта моделирования, т. е. системы 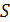 , можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:
, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:
- совокупность входных воздействий на систему: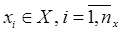
- совокупность воздействий внешней среды: 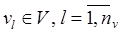 ;
;
- совокупность внутренних (собственных) параметров системы: 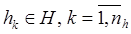 ;
;
- совокупность выходных характеристик системы: 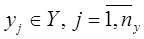 .
.
Внешняя среда

 |
Входные воздействия Выходные характеристики
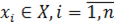
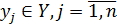
Рисунок 4. Модель объекта моделирования
При моделировании системы 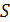 входные воздействия, воздействия внешней среды
входные воздействия, воздействия внешней среды 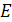 и внутренние параметры системы являются независимыми (экзогенными) переменными,которые в векторной форме имеют соответственно вид:
и внутренние параметры системы являются независимыми (экзогенными) переменными,которые в векторной форме имеют соответственно вид: 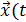 )=
)= 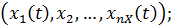
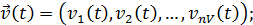
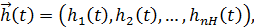
а выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид:
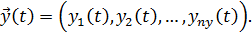
Процесс функционирования системы 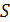 описывается во времени оператором
описывается во времени оператором 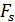 ,который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида:
,который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида:
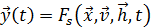 . (1)
. (1)
Совокупность зависимостей выходных характеристик системы от времени 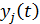 для всех видов
для всех видов 
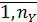 называется выходной траекторией
называется выходной траекторией 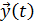 . Зависимость (1) называется законом функционированиясистемы
. Зависимость (1) называется законом функционированиясистемы 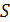 и обозначается
и обозначается 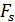 . В общем случае закон функционирования системы
. В общем случае закон функционирования системы 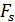 может быть задан в виде функции, функционала,логических условий, в алгоритмической и табличной формахили в виде словесного правила соответствия.
может быть задан в виде функции, функционала,логических условий, в алгоритмической и табличной формахили в виде словесного правила соответствия.
Весьма важным для описания и исследования системы 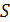 является понятие алгоритма функционирования
является понятие алгоритма функционирования 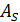 ,под которым понимаетсяметод получения выходных характеристик с учетом входных воздействий
,под которым понимаетсяметод получения выходных характеристик с учетом входных воздействий 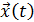 , воздействий внешней среды
, воздействий внешней среды 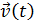 и собственныхпараметров системы
и собственныхпараметров системы 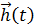 . Очевидно, что один и тот же закон функционирования
. Очевидно, что один и тот же закон функционирования 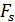 системы
системы 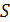 может быть реализован различнымиспособами, т. е. с помощью множества различных алгоритмовфункционирования
может быть реализован различнымиспособами, т. е. с помощью множества различных алгоритмовфункционирования 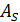 .
.
Соотношение (1) является математическим описанием поведения объекта (системы) моделирования во времени  , т.е. отражает его динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями.
, т.е. отражает его динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями.
Для статических моделей математическая модель (1) представляет собой отображение между двумя подмножествами свойств моделируемого объекта 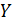 и
и 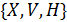 , что в векторной форме может быть записано как
, что в векторной форме может быть записано как
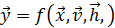 . (2)
. (2)
Соотношения (1) и (2) могут быть заданы различными способами: аналитически (с помощью формул), графически, таблично и т. д. Такие соотношения в ряде случаев могут быть получены через свойства системы 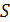 в конкретные моменты времени, называемые состояниями. Состояние системы S характеризуется векторами
в конкретные моменты времени, называемые состояниями. Состояние системы S характеризуется векторами 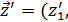
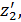 …,
…, 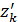 ) и
) и 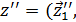
 …,
…,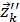 ), где
), где
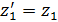 (
(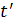 ),
), 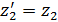 (
(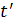 ), …,
), …, 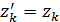 (
(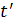 ) в момент
) в момент 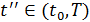 ;
;
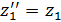 (
(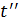 ),
), 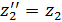 (
(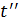 ), …,
), …, 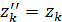 (
(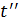 ) в момент
) в момент 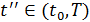 ,
, 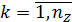 .
.
Если рассматривать процесс функционирования системы S как
последовательную смену состояний 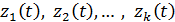 , то они могут быть интерпретированы как координаты точки в
, то они могут быть интерпретированы как координаты точки в 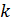 - мерном фазовом пространстве, причем каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний
- мерном фазовом пространстве, причем каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний 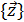 называется пространством состояний объекта моделирования Z, причем
называется пространством состояний объекта моделирования Z, причем  .
.
Состояния системы 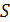 в момент времени
в момент времени 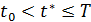 полностью определяются начальными условиями
полностью определяются начальными условиями 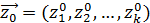 , [где
, [где  ],входными воздействиями
],входными воздействиями 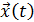 , внутренними параметрами
, внутренними параметрами 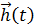 и воздействиями внешней среды
и воздействиями внешней среды 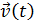 , которые имели место за промежуток времени
, которые имели место за промежуток времени 
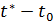 , с помощью двух векторных уравнений:
, с помощью двух векторных уравнений:
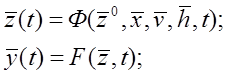
Первое уравнение по начальному состоянию 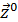 и экзогенным переменным
и экзогенным переменным 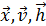 определяет вектор-функцию
определяет вектор-функцию 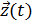 ,а второе по полученному значению состояний
,а второе по полученному значению состояний 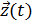 - эндогенные переменные на выходе системы
- эндогенные переменные на выходе системы 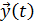 . Таким образом, цепочка уравнений объекта
. Таким образом, цепочка уравнений объекта
«вход – состояния – выход»
позволяет определить характеристики системы:
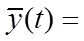
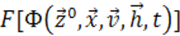 .
.
Таким образом, под математической моделью объекта(реальной системы) понимают конечное подмножество переменных {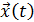 ,
, 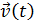 ,
, 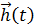 } вместе с математическими связями между ними и характеристиками
} вместе с математическими связями между ними и характеристиками 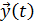 .
.
Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, т.е. стохастические (вероятностные) воздействия внешней среды 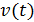 и стохастические внутренние параметры
и стохастические внутренние параметры 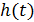 отсутствуют, то модель называется детерминированной (определенной)в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями
отсутствуют, то модель называется детерминированной (определенной)в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями
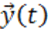
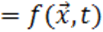 .
.
Очевидно, что детерминированная модель является частным случаем стохастической модели.
 2014-02-02
2014-02-02 2769
2769








