МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН
Результаты имитационного моделирования, как правило, представляют собой оценки значений функциональных характеристик имитируемой системы. Поэтому основой метода имитационного моделирования является моделирование случайных величин с заданными законами распределения и случайных событий с заданными вероятностями реализаций.
Массовые явления или процессы характеризуются многократным повторением при постоянных условиях некоторых опытов. Абстрагируясь от специальных свойств этих опытов, в теории вероятностей вводится понятие испытания. Испытанием называется осуществление определенного комплекса условий, который может быть воспроизведен сколь угодно большое число раз. Явления, происходящие в результате испытания, называются событиями.
Положительное число в отрезке [0,1], представляющее собой количественную меру возможности появления случайного события в испытании, называется его вероятностью. Вероятность появления события 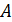 обозначают символом
обозначают символом 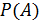 , причем
, причем 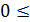
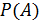
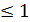 . Вероятность понимается как идеальная мера возможности появления события.
. Вероятность понимается как идеальная мера возможности появления события.
Случайная величина рассматривается как функция, аргументом которой служит элементарное случайное событие. Случайная величина называется:
· дискретной, если множество ее возможных значений счетное;
· непрерывной, если множество ее возможных значений несчетное.
Математическое ожидание 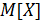 характеризует среднее значение случайной величины
характеризует среднее значение случайной величины 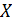 и определяется по формулам:
и определяется по формулам: 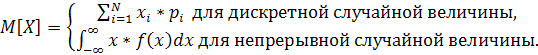
Дисперсия случайной величины 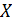 характеризует степень разброса значений случайной величины относительно ее математического ожидания и определяется по формуле:
характеризует степень разброса значений случайной величины относительно ее математического ожидания и определяется по формуле: 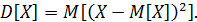
Среднее квадратическое отклонение случайной величины 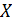 характеризует ширину диапазона значений
характеризует ширину диапазона значений 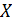 и равно
и равно 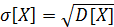 .
.
Универсальным способом задания случайной величины 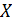 является функция распределения – вероятность того, что
является функция распределения – вероятность того, что 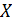 примет значение меньшее, чем аргумент функции
примет значение меньшее, чем аргумент функции 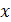 :
: 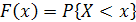 .
.
Распределение случайной величины 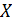 – это функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
– это функция, которая однозначно определяет вероятность того, что случайная величина принимает заданное значение или принадлежит к некоторому заданному интервалу.
Для непрерывной случайной величины 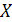 , имеющей дифференцируемую функцию распределения
, имеющей дифференцируемую функцию распределения 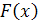 , функция плотности вероятности равна
, функция плотности вероятности равна 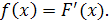
Генеральной совокупностью называется множество объектов, на которых рассматривается изучаемый признак. Количество объектов в генеральной совокупности называется ее объемом и обозначается 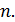
Выборкой называется множество объектов, случайным образом выбранных из генеральной совокупности. Количество объектов в выборке называется ее объемом и обозначается 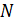 .
.
Вариационным рядом называется таблица, состоящая из конкретных значений изучаемого признака, входящих в выборку, и соответствующих им кратностей (частот):
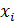 | 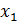 | 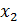 | … |  |
 | 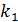 | 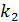 | … | 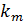 |
Для вариационного ряда определяются:
- выборочное среднее 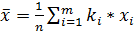 ;
;
Коэффициент корреляциипоказывает, какой процент составляет стандартное отклонение от выборочного среднего и служит для сравнения признаков, имеющих разные измерения.
На генеральной совокупности признак 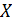 характеризуется генеральным параметром
характеризуется генеральным параметром 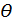 , в котором может быть математическое ожидание
, в котором может быть математическое ожидание 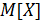 или среднее квадратическое отклонение
или среднее квадратическое отклонение 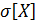 . В силу большого объема генеральной совокупности, значение генерального параметра
. В силу большого объема генеральной совокупности, значение генерального параметра 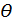 не может быть вычислено. Поэтому для оценки генерального параметра используется выборочный параметр
не может быть вычислено. Поэтому для оценки генерального параметра используется выборочный параметр 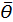 , которым может являться выборочное среднее или стандартное отклонение.
, которым может являться выборочное среднее или стандартное отклонение.
Для генерального параметра 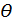 интервал
интервал 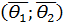 является доверительным интервалом, а вероятность
является доверительным интервалом, а вероятность 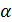 – доверительной вероятностью, если справедливо равенство
– доверительной вероятностью, если справедливо равенство 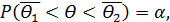 где
где 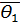 и
и 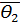 вычисляются на основании выборочных данных.
вычисляются на основании выборочных данных.
Доверительный интервал для математического ожидания имеет вид 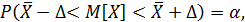 где
где 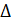 – предельная ошибка выборки. Она равна:
– предельная ошибка выборки. Она равна:
- для бесповторной выборки, когда отобранный объект после обследования не возвращается в генеральную совокупность: 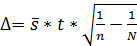 ;
;
- для повторной выборки, когда отобранный объект после обследования возвращается в генеральную совокупность: 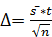 , (
, (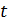 находится по таблице).
находится по таблице).
Доверительный интервал для среднеквадратического отклонения 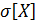 имеет вид:
имеет вид: 
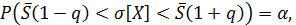 при
при 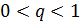 ;
; 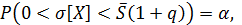 при
при 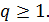
 2014-02-02
2014-02-02 1429
1429

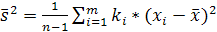 ;
;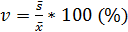 .
.