Данные уравнения в общем случае имеют вид
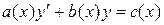 ,
,
где 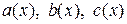 - непрерывные функции.
- непрерывные функции.
Разделим уравнение на 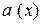 , получим
, получим
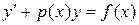 ,
,
где 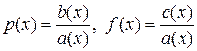 .
.
Известны два метода решения этих уравнений.
1. Методзамены переменной.
Искомую функцию заменяют на произведение двух функций
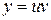 ,
,
где 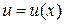 ,
, 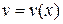 - некоторые неизвестные дифференцируемые функции.
- некоторые неизвестные дифференцируемые функции.
Подставим 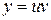 в уравнение, получим
в уравнение, получим 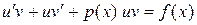 . Третье слагаемое
. Третье слагаемое 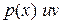 сгруппируем с одним из первых слагаемых, либо с
сгруппируем с одним из первых слагаемых, либо с 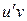 , либо с
, либо с 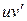 . Функции
. Функции 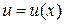 и
и 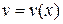 входят в уравнение замены симметрично. Пусть объединим первое и третье слагаемые
входят в уравнение замены симметрично. Пусть объединим первое и третье слагаемые
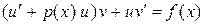 .
.
Искомой является одна функция 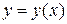 , а введены с помощью замены две
, а введены с помощью замены две 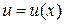 ,
, 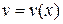 , поэтому одну из них, пусть
, поэтому одну из них, пусть 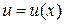 , выберем по своему усмотрению так, чтобы
, выберем по своему усмотрению так, чтобы 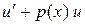 равнялось нулю. Тогда уравнение распадется на два уравнения, каждое из которых с разделяющимися переменными,
равнялось нулю. Тогда уравнение распадется на два уравнения, каждое из которых с разделяющимися переменными,
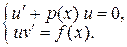
Необходимо сначала решить первое уравнение, найти функцию 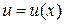 . Затем подставить эту функцию во второе уравнение и решить его.
. Затем подставить эту функцию во второе уравнение и решить его.
Решаем первое уравнение. При решении этого уравнения достаточно найти не общее решение, а одно какое-либо частное решение
 Þ
Þ 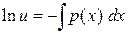 Þ
Þ 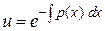 .
.
Подставим найденную функцию 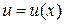 во второе уравнение
во второе уравнение 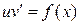 и решим его. Найдем функцию
и решим его. Найдем функцию 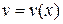 .
.
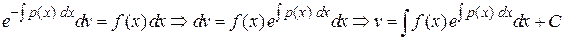 .
.
Затем записываем решение исходного уравнения как произведение функций 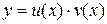 .
.
 .
.
Получена конечная формула для нахождения общего решения линейного уравнения. Однако, при решении примеров, обычно, используют замену 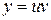 и повторяют приведенные выше действия.
и повторяют приведенные выше действия.
Пример 7.12. Решить уравнение 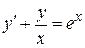 .
.
Используем подстановку 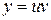 , получаем
, получаем
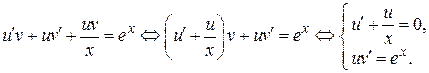
Решаем первое уравнение системы
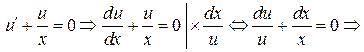
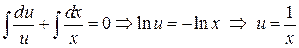 .
.
Решаем второе уравнение системы 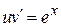 .
.
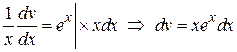 Þ
Þ 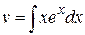 .
.
Интеграл находим методом интегрирования по частям
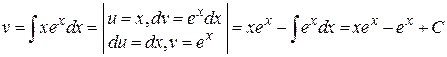 Þ
Þ 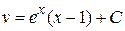 .
.
Находим общее решение исходного уравнения 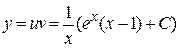 ;
;
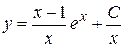 .
.
2. Метод вариации произвольной постоянной.
Для нахождения общего решения неоднородного линейного уравнения
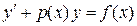
сначала решают соответствующее однородное уравнение
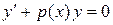 .
.
Данное уравнение с разделяющимися переменными. Решая его, получим
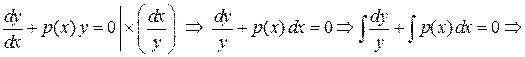
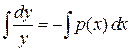 Þ
Þ 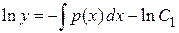 Þ
Þ
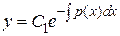 .
.
Далее, произвольную постоянную 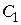 заменяют на функцию
заменяют на функцию 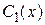 и ищут решение исходного неоднородного уравнения в виде
и ищут решение исходного неоднородного уравнения в виде
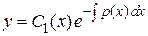 .
.
Теперь, чтобы получить решение уравнения, необходимо найти функцию 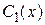 . Найдем производную функции
. Найдем производную функции 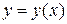 .
.
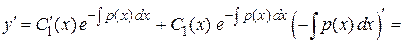
 .
.
Подставим функцию 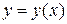 и ее производную в исходное неоднородное уравнение
и ее производную в исходное неоднородное уравнение 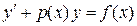 .
.
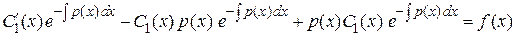 .
.
Второе и третье слагаемые в левой части этого уравнения уничтожаются, получается дифференциальное уравнение относительно функции 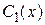 с разделяющимися переменными
с разделяющимися переменными
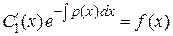 .
.
Разделяем переменные и интегрируем
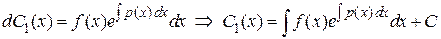 ,
,
где С – произвольная постоянная.
Записываем решение исходного неоднородного уравнения
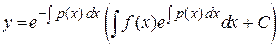 .
.
Пример 7.13. Найти общее решение уравнения 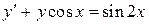 .
.
Используем метод вариации произвольной постоянной. Решим соответствующее исходному однородное уравнение
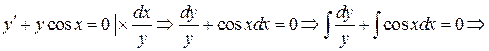
 .
.
Ищем решение исходного неоднородного уравнения в виде 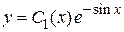 . Подставляем эту функцию в исходное уравнение
. Подставляем эту функцию в исходное уравнение
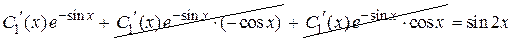 .
.
Получаем уравнение для нахождения 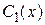
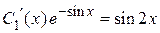 .
.
Решаем это уравнение
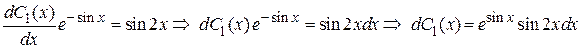 .
.
Находим
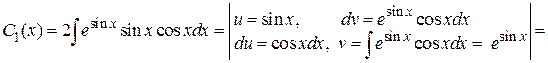
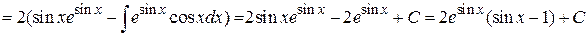 .
.
Записываем решение исходного уравнения
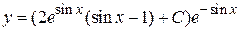
или
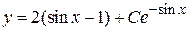 .
.
 2014-02-02
2014-02-02 551
551








