В общем случае дифференциальное уравнение n -ого порядка имеет вид
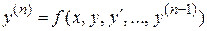 или
или 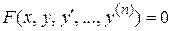 .
.
Теорема 7.2 о существовании и единственности решения.
Если в дифференциальном уравнении 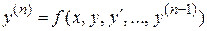 функция
функция 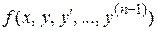 и ее частные производные
и ее частные производные 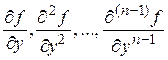
являются непрерывными в некоторой области D, то для любой точки 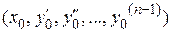 , принадлежащей этой области, существует единственное решение уравнения, удовлетворяющее начальным условиям
, принадлежащей этой области, существует единственное решение уравнения, удовлетворяющее начальным условиям
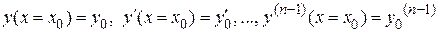 .
.
Если условия данной теоремы выполняются, то геометрически решение дифференциального уравнения n -ого порядка представляет кривую, проходящую через точку 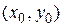 в направлении
в направлении 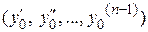 .
.
7. 10. Дифференциальное уравнение вида 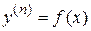
Уравнение данного вида решается путем повторного интегрирования n раз.
Интегрируем уравнение
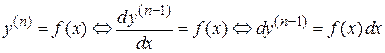 Þ
Þ
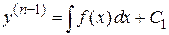 ;
;
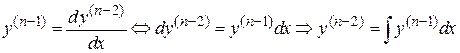 ;
;
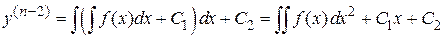 .
.
Аналогично можно получить
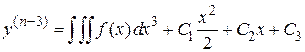 ,
,
……………………………………………………………………
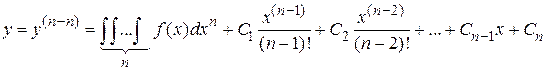 .
.
Пример 7.16. Решить дифференциальное уравнение  при начальных условиях
при начальных условиях 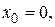
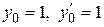 .
.
Находим 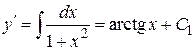 . Подставим
. Подставим 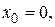
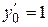 , получим
, получим 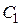 .
.
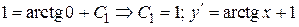 .
.
Находим 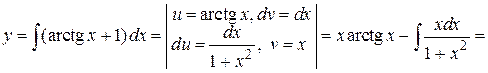 =
=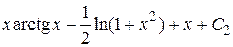 .
.
Подставим начальные значения 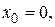
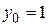 в полученное равенство, найдем значение
в полученное равенство, найдем значение 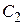 .
. 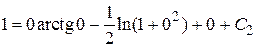 Þ
Þ 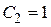 .
.
Таким образом, общее решение
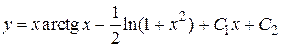 ,
,
Частное решение, удовлетворяющее заданным начальным условиям
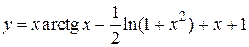 .
.
 2014-02-02
2014-02-02 615
615








