Дифференциальные уравнения первого порядка
Данные уравнения в общем случае имеют вид
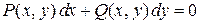 ,
,
где левая часть представляет полный дифференциал некоторой функции 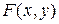 .
.
Известно, что полный дифференциал функции равен
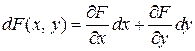 .
.
Если левая часть заданного уравнения равна 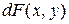 , то уравнение можно записать в виде
, то уравнение можно записать в виде 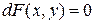 . Тогда общий интеграл (общее решение в неявном виде) данного уравнения будет определяться уравнением
. Тогда общий интеграл (общее решение в неявном виде) данного уравнения будет определяться уравнением 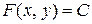 , где С – произвольная постоянная.
, где С – произвольная постоянная.
Необходимым и достаточным условием того, чтобы выражение
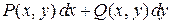
являлось полным дифференциалом, служит равенство
 .
.
Если это условие выполняется, то
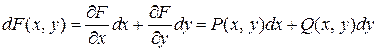 .
.
Отсюда следует
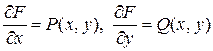 .
.
Интегрируем соотношение 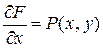 по x, находим
по x, находим
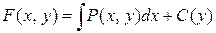 ,
,
где 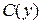 - произвольная функция, зависящая от y.
- произвольная функция, зависящая от y.
Функцию С (y) необходимо выбрать так, чтобы выполнялось второе условие существования полного дифференциала
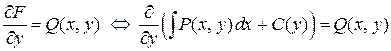 .
.
Дифференцируем по y, имеем  .
.
Отсюда получаем дифференциальное уравнение для нахождения функции С (y)
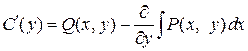 .
.
Интегрируем данное уравнение, находим С (y) и подставляем егов ранее полученное выражение 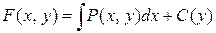 .
.
Получим общий интеграл
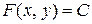 или
или 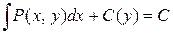 .
.
Если имеются начальные условия для нахождения частного решения 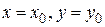 , то необходимо найти
, то необходимо найти 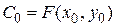 и записать частный интеграл
и записать частный интеграл 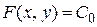 .
.
Пример 7.15. Для уравнения 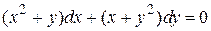 найти общий интеграл и частный интеграл, удовлетворяющий условиям
найти общий интеграл и частный интеграл, удовлетворяющий условиям 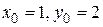 .
.
Проверим условие существования полного дифференциала. Находим
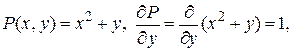
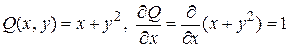 .
.
Условие 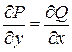 выполняется 1 = 1.
выполняется 1 = 1.
Находим
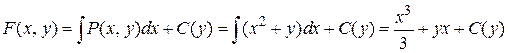 .
.
Находим частную производную от этой функции
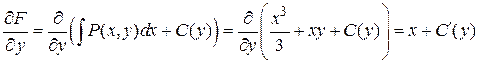 .
.
Приравниваем 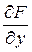 к
к 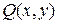 , получаем уравнение для нахождения
, получаем уравнение для нахождения 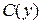 .
.
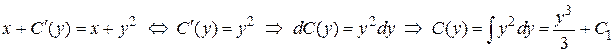 ,
,
где 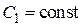 .
.
Записываем 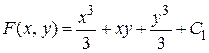 .
.
Общий интеграл исходного уравнения 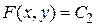 имеет вид
имеет вид
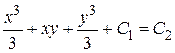 , где
, где 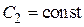 ,
,
или
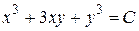 , где
, где 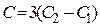 .
.
Находим значение произвольной постоянной С, соответствующее начальным условиям 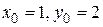 ,
,
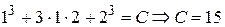 .
.
Частный интеграл
 .
.
Таким образом, общий и частный интегралы имеют вид
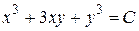 ,
,  .
.
 2014-02-02
2014-02-02 1164
1164








