В общем случае дифференциальное уравнение первого порядка имеет вид
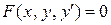 или
или 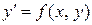 .
.
Используя уравнение 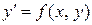 , можно найти производную искомой функции в любой точке области определения функции
, можно найти производную искомой функции в любой точке области определения функции 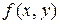 на плоскости
на плоскости 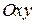 . Эта производная определяет тангенс угла наклона касательной к интегральной кривой. Поэтому можно в каждой точке плоскости
. Эта производная определяет тангенс угла наклона касательной к интегральной кривой. Поэтому можно в каждой точке плоскости 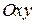 построить поле направлений и изобразить приближенно семейство интегральных кривых. Для этого используют изоклины.
построить поле направлений и изобразить приближенно семейство интегральных кривых. Для этого используют изоклины.
Изоклиной называется линия, на которой производная 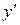 решения дифференциального уравнения принимает постоянное значение.
решения дифференциального уравнения принимает постоянное значение.
Уравнение изоклин для уравнения 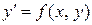 имеет вид
имеет вид 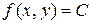 , где
, где 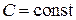 .
.
Пример 7.5. Для дифференциального уравнения 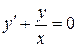 построить поле направлений, несколько изоклин и приближенный вид интегральных кривых.
построить поле направлений, несколько изоклин и приближенный вид интегральных кривых.
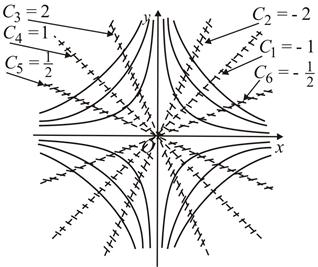 Рис. 81 Рис. 81 | Уравнение изоклин имеет вид 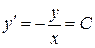 , т. е. , т. е. 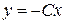 . На рисунке (рис. 81) изображены изоклины при . На рисунке (рис. 81) изображены изоклины при 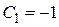 , , 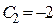 , , 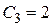 , ,  , , 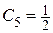 , ,  . Например, уравнение изоклины . Например, уравнение изоклины 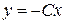 при при  является прямой является прямой  , проходящей по биссектрисе 1-го координатного угла. Тангенс угла наклона касательной к интегральной кривой на этой изоклине равен , проходящей по биссектрисе 1-го координатного угла. Тангенс угла наклона касательной к интегральной кривой на этой изоклине равен |
 (
(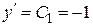 ), т. е. касательные образуют с осью
), т. е. касательные образуют с осью 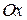 угол 135°. На рисунке это направление отмечено черточками.
угол 135°. На рисунке это направление отмечено черточками.
При  уравнение изоклины
уравнение изоклины  . Тангенс угла наклона касательных к интегральной кривой на этой изоклине равен
. Тангенс угла наклона касательных к интегральной кривой на этой изоклине равен  . Уравнения изоклин: при
. Уравнения изоклин: при 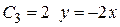 , при
, при  , при
, при 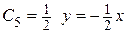 , при
, при  . Чтобы изобразить приближенно вид интегральной кривой, необходимо выбрать произвольно начальную точку и от нее провести линию (кривую). Эта линия должна касаться направлений (черточек) на изоклинах.
. Чтобы изобразить приближенно вид интегральной кривой, необходимо выбрать произвольно начальную точку и от нее провести линию (кривую). Эта линия должна касаться направлений (черточек) на изоклинах.
 2014-02-02
2014-02-02 4081
4081
