Задача Коши. Теорема о существовании и единственности решения
Задача Коши для дифференциального уравнения 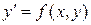 заключается в нахождении решения
заключается в нахождении решения 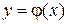 , удовлетворяющего заданным начальным условиям
, удовлетворяющего заданным начальным условиям 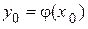 . Иначе говоря, требуется найти интегральную кривую, проходящую через заданную точку
. Иначе говоря, требуется найти интегральную кривую, проходящую через заданную точку 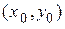 .
.
Теорема 7.1 (без доказательства). Если для дифференциального уравнения 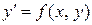 функция
функция 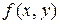 и ее частная производная
и ее частная производная 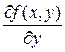 являются непрерывными в некоторой области D, то для любой точки этой области
являются непрерывными в некоторой области D, то для любой точки этой области 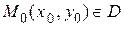 существует единственное решение
существует единственное решение 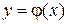 , удовлетворяющее условию
, удовлетворяющее условию 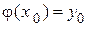 .
.
Пример 7.6. Для дифференциального уравнения 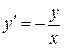 найти частное решение, проходящее через точку
найти частное решение, проходящее через точку 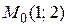 . Общим решением этого уравнения (см. пример 7.1) является функция
. Общим решением этого уравнения (см. пример 7.1) является функция 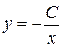 . Подставляем значения
. Подставляем значения 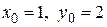 в общее решение, получим
в общее решение, получим 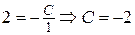 . Подставляем
. Подставляем 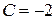 в общее решение, записываем частное решение
в общее решение, записываем частное решение 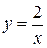 .
.
 2014-02-02
2014-02-02 961
961








