В общем случае уравнение Бернулли имеет вид
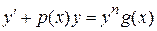 ,
, 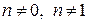 ,
,
здесь 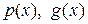 - непрерывные функции.
- непрерывные функции.
Поделим уравнение на 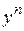 , получим
, получим
 .
.
Данное уравнение приводится к линейному уравнению с помощью подстановки
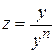 или
или 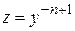 .
.
Найдем 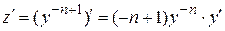 Þ
Þ 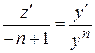 и подставим в исходное уравнение, получим линейное уравнение относительно переменной z.
и подставим в исходное уравнение, получим линейное уравнение относительно переменной z.
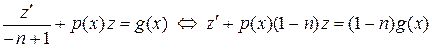 .
.
Далее уравнение может быть разрешено известными методами решения линейного уравнения. Однако уравнение Бернулли может быть решено без замены переменной непосредственно с помощью подстановки 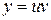 .
.
Пример 7.14. Решить уравнение 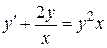 .
.
Используем подстановку 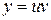 .
.
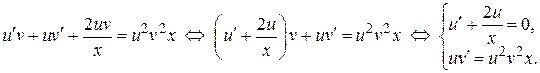
Решаем первое уравнение системы
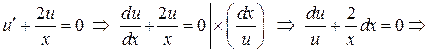
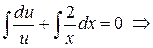
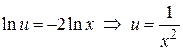 .
.
Решаем второе уравнение системы
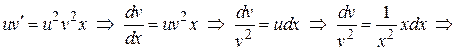
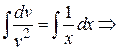
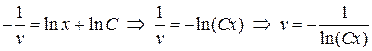 .
.
Записываем решение исходного уравнения 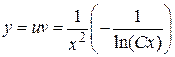 или
или
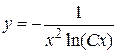 .
.
 2014-02-02
2014-02-02 666
666








