2014-02-02
846
1. Сходимость числового ряда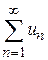 
не нарушится, если все его члены умножить на некоторое отличное от нуля число l; причем
.
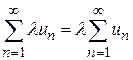Д о к а з а т е л ь с т в о. Используем определение суммы ряда и свойства пределов, получаем
.
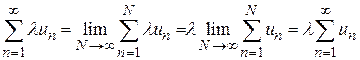2. При сложении соответствующих членов двух сходящихся рядов 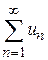и 
получится сходящийся ряд; причем
.
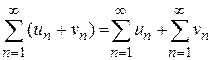Д о к а з а т е л ь с т в о. Используем определение суммы ряда и свойства пределов, получаем
.
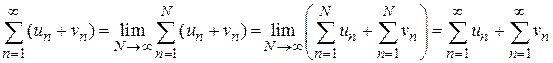3. Сходимость ряда не нарушится, если отбросить конечное число его членов.
Д о к а з а т е л ь с т в о. Пусть сумма ряда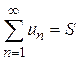 
. Не нарушая общности можно считать, что отбрасываются k первых его членов, сумма которых 
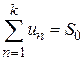. Так как ряд сходящийся, то 
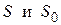являются конечными величинами, поэтому 
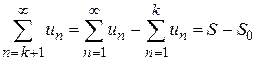так же является конечной величиной и, следовательно, ряд 
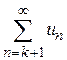сходится.
Отсюда также следует, что если в расходящемся ряде отбросить конечное число членов, то ряд останется расходящимся.
