2014-02-02
2072
Теорема 8.1. Если числовой ряд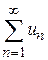 
сходится, то его общий член 
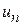при неограниченном возрастании его номера стремится к нулю, т. е. 
.
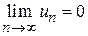Д о к а з а т е л ь с т в о. Представим общий член 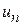как разность частичных сумм и найдем предел
.
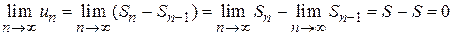Следствие. Если предел общего члена ряда при неограниченном возрастании его номера отличен от нуля, т. е.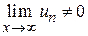 
, то ряд расходится.
Пример 8.2. Используя следствие из необходимого признака сходимости показать, что ряд 
расходится.
Находим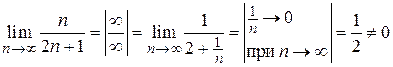 
.
Следовательно, ряд расходится.
Данный необходимый признак сходимости числовых рядов не позволяет установить сходимость ряда. Он позволяет только установить, что ряд расходится, и только для тех рядов, которые расходятся достаточно быстро.
Пример 8.3. Рассмотрим ряд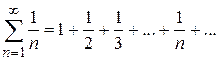 
. Данный ряд часто используется при исследовании сходимости числовых рядов и имеет специальное название «гармонический». Для данного ряда выполняется необходимый признак, так как 
. Однако данный ряд расходится. Покажем это.
Так как ряд имеет бесконечное число членов, то из его членов можно сформировать бесконечное число групп (сумм), сумма каждой из которых больше 1/2. Группы членов ряда заключены в скобки. В первую группу входит 2 члена, во вторую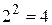 
, в третью 
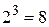и т. д.
|
|
|
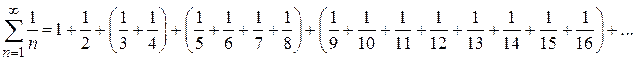В каждой группе заменим все слагаемые последними, которые является наименьшими в группах, получим неравенство
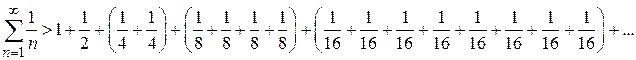Так как сумма дробей в каждой скобке равняется ½, имеем
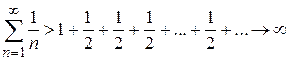при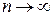 
, т. е. ряд расходится.
Необходимо также отметить, что если отбросить любое конечное (большое) число членов этого ряда, сумма его останется бесконечно большой.
