Основные понятия
Глава 8. Числовые ряды
Множество чисел перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров называется числовой последовательностью
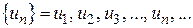 .
.
Числовым рядом называется сумма членов бесконечной числовой последовательности
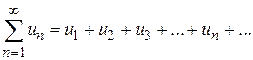 .
.
Ряд считается заданным, если известен закон образования n -го (общего) члена ряда в зависимости от его номера. Обычно общий член ряда задается как функция 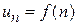 или
или 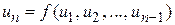 .
.
Например: 1) если 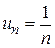 , то
, то 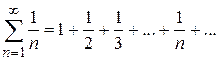 ;
;
2) если 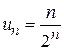 , то
, то 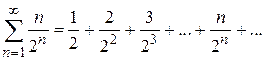 ;
;
3) если 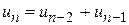 ,
, 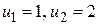 , то
, то
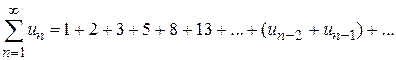 .
.
Обычно, при исследовании числовых рядов возникает необходимость нахождения вида общего члена ряда как функции от номера этого члена. Для этого нужно перенумеровать члены ряда и, учитывая четность, периодичность и другие особенности его членов записать функцию 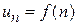 .
.
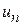 | 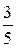 + + | 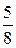 + + | 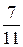 + + | …. + | 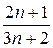 + … + … |
| n | ××× | n |
Например: 1)
Числитель каждого следующего члена этого ряда на 2 больше, а знаменатель на 3 больше, поэтому в n -ом члене ряда нужно записать в числителе 2 n, а в знаменателе 3 n. Кроме того, в числителе нужно к 2 n прибавить 1, а в знаменателе к 3 n прибавить 2, чтобы при n = 1 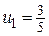 . Тогда
. Тогда  .
.
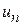 | 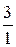 + + | 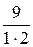 + + | 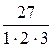 + + | …. + | 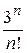 + … + … |
| n | ××× | n |
2)
Числители являются степенями числа 3, а в знаменателях находится факториалы номеров членов n, 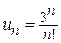 .
.
 2014-02-02
2014-02-02 1770
1770








