Теорема 8. 5. Если для знакоположительного ряда 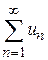 существует предел отношения последующего члена ряда к предыдущему при неограниченном возрастании их номеров, т. е. существует предел
существует предел отношения последующего члена ряда к предыдущему при неограниченном возрастании их номеров, т. е. существует предел 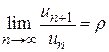 , то:
, то:
1) если r < 1, то ряд сходится; 2) если r > 1, то ряд расходится;
3) если r = 1, то данный признак не позволяет решить вопрос о сходимости ряда (ряд может как сходиться, так и расходиться).
Д о к а з а т е л ь с т в о.1. Пусть  . Если r < 1, то всегда найдется число q, удовлетворяющее неравенству r < q < 1. В этом случае по определению предела существует такое число N, что если номер члена ряда n > N, то отношение
. Если r < 1, то всегда найдется число q, удовлетворяющее неравенству r < q < 1. В этом случае по определению предела существует такое число N, что если номер члена ряда n > N, то отношение 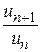 меньше этого числа q, т.е.
меньше этого числа q, т.е. 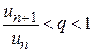 . Данное неравенство представим в следующем виде
. Данное неравенство представим в следующем виде 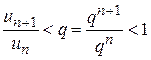 . Отношение
. Отношение 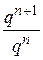 является отношением последующего члена ряда к предыдущему для бесконечной убывающей геометрической прогрессии
является отношением последующего члена ряда к предыдущему для бесконечной убывающей геометрической прогрессии 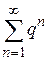 , которая сходится, так как знаменатель прогрессии меньше единицы (q < 1). В соответствии с теоремой 8.4 (третий признак сравнения рядов) ряд
, которая сходится, так как знаменатель прогрессии меньше единицы (q < 1). В соответствии с теоремой 8.4 (третий признак сравнения рядов) ряд 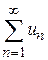 сходится.
сходится.
2. Пусть 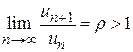 . Тогда существует такое число q, которое больше единицы, но меньше r, т. е.
. Тогда существует такое число q, которое больше единицы, но меньше r, т. е. 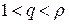 . В этом случае существует такое число N, что если номер члена ряда n > N, то отношение
. В этом случае существует такое число N, что если номер члена ряда n > N, то отношение 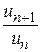 больше q, т. е.
больше q, т. е. 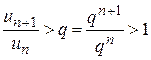 . Тогда по теореме 8.4 ряд
. Тогда по теореме 8.4 ряд 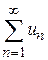 расходится.
расходится.
Данный признак Даламбера является наиболее простым и часто применяемым. Однако он дает ответ на вопрос о сходимости ряда только в тех случаях, когда ряд достаточно быстро сходится или расходится.
Пример 8.7. Исследовать сходимость ряда 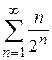 .
.
Находим 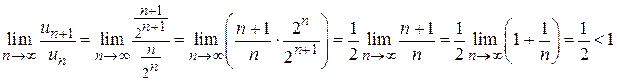 . Следовательно, ряд сходится.
. Следовательно, ряд сходится.
Пример 8.8. Исследовать сходимость ряда 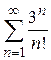 .
.
Находим
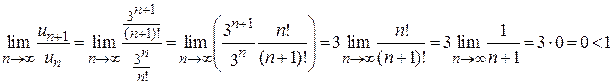 .
.
Ряд сходится.
Пример 8.9. Исследовать сходимость ряда 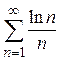 .
.
Найдем предел 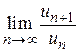 . При этом воспользуемся правилом Лопиталя.
. При этом воспользуемся правилом Лопиталя.
Находим

 .
.
В данном случае признак Даламбера не позволяет решить вопрос о сходимости ряда.
Пример 8.10. Исследовать сходимость ряда 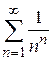 .
.
Найдем предел 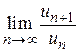 . При этом воспользуемся вторым замечательным пределом. Находим
. При этом воспользуемся вторым замечательным пределом. Находим
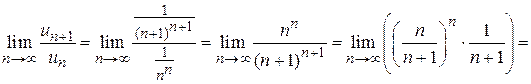
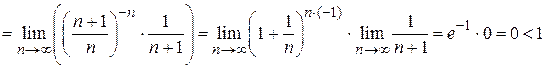 .
.
Следовательно, ряд сходится.
Пример 8.11. Исследовать сходимость ряда 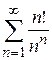 .
.
Находим
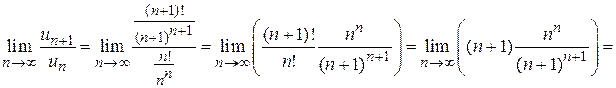
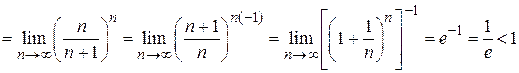 .
.
Ряд сходится.
 2014-02-02
2014-02-02 4598
4598
