Гидростатика

Элементы физической гидромеханики

Физическая гидромеханика – это раздел физики, изучающий законы движения жидкостей и газов применительно к решению прикладных задач.

Исторически основным объектом гидромеханики считалась вода. Это связано с распространенностью и большим значением водной среды в практической деятельности (водоснабжение, орошение, создание гидравлических машин, гидроэнергетика, и т.д.). С течением времени содержание гидромеханики изменилось, и она стала использоваться при расчетах потоков других жидкостей, как в природных, так и технических устройствах.

В состав современной физической гидромеханики входит три основных раздела: гидростатика – изучает законы равновесия жидких тел; гидродинамика – рассматривает общие законы движения жидкостей; раздел, посвященный приложению законов движения жидкостей к конкретным задачам (строится в основном на опытных положениях и зависимостях, а также на эмпирических определениях значений различных коэффициентов, характеризующих течение в различных природных и технических системах).

Современная гидромеханика основное внимание сосредоточивает на создании теории турбулентных течений, разработке методов описания нелинейной динамики движения жидкостей с использованием синергетических представлений.

Гидростатика – теория равновесия жидкостей и газов относительно выбранной системы координат. В гидростатике рассматриваются задачи двух типов. В первом типе задач определяется пространственное распределение давления и плотности, конфигурация свободной поверхности водной среды в условиях покоя. Во втором типе задач производится расчет силового воздействия покоящейся жидкости на расположенные в ней тела.

Состояние покоя жидкости определяется равенством всех сил, действующих на ее частицы. Это условие может быть реализовано как в неподвижной системе координат (связанной с землей), так и в подвижной системе отсчета (например, закрепленной на стенках подвижных резервуаров). Равновесное состояние жидкости, находящейся в покое относительно неподвижной системы координат, называется абсолютным покоем, а в подвижной – относительным покоем. Современные проблемы гидростатики связаны с необходимостью исследований относительного покоя применительно к задачам гидрофизики, гравитации, астрофизики.

Построение гидростатической модели подразумевает составление системы дифференциальных уравнений, определяющих сохранение массы, баланс сил и постоянство полной энергии. Кроме этого, в этих уравнениях необходимо принять скорость жидкости равной нулю, определить связь напряжений поверхностных сил со скоростями деформации жидких частиц, задать связь пространственного распределения плотности, температуры и давления.

При равновесии 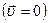из уравнения неразрывности следует, что 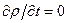, т.е. в выбранной системе отсчета (например, декартовой системе координат) поле плотности стационарно: .

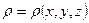В случае равновесия уравнения Эйлера и Навье – Стокса приводят к уравнению

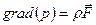, (7.1)

или

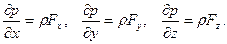
Если 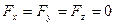, то 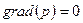, т.е. давление 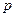во всех точках в жидкости или газе одинаково. Это утверждение выражает закон Паскаля.

Вспоминая про потенциальность поля скорости, на основе (7.1) по аналогии можно сделать вывод о том, что поле при равновесии не может быть произвольным. В общем случае из (7.1) получим

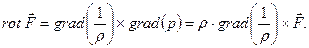
Отсюда следует, что

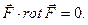(7.2)

Соотношение (7.2) представляет собой необходимое условие для поля сил 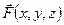, при котором возможно равновесие.

При , 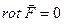. Это означает, что силы должны обладать потенциалом 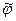, т.е. 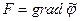. Отсюда ясно, что однородная несжимаемая жидкость может находиться в равновесии только в потенциальном поле внешних массовых сил.

Для сжимаемой среды, если поле сил потенциально, из (7.1) получим

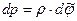. (7.3)

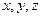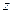Пусть в декартовой системе координат ось направлена вертикально вверх. Тогда 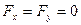, , 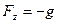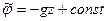и 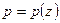, 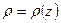. Согласно уравнению состояния 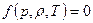получаем, что температура в тяжелой покоящейся жидкости также зависит только от координаты 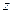, т.е. .

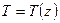На основе (7.1),

.

На основе (7.3),

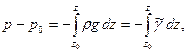(7.4)

где 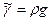– удельный вес жидкости.

Рассмотрим уравнения 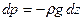и . Имеем:

,

откуда для определения давления 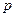получим

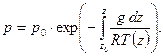(7.5)

Принимая (однородная атмосфера), параметры 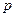и 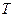будут линейными функциями 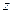и найдется такая высота , на которой :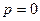

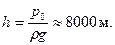
Принимая, что атмосфера находится в изотермическом равновесии 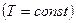, на основе (7.5),

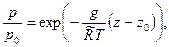
и в данном случае высота изотермической атмосферы получается бесконечной.

Часто принимают, что до высот около 11 км температура с высотой в атмосфере убывает по линейному закону

(7.6)

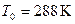где – абсолютная температура при (обычно принимают ), а 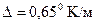– величина, на которую убывает температура при подъеме на каждые 100 м.

Принимая такое распределение температуры с высотой, получим

(7.7)

высота атмосферы получается конечной, т.к. 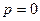при 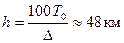. Поэтому допущение (7.6) неприемлемо для всей атмосферы. Из (7.7) на основе (7.6) запишем

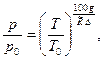
а из уравнения Клапейрона:

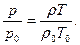
Поэтому

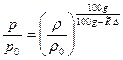, или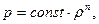

где .

Условие теплового равновесия среды получаем из уравнения притока тепла, которое при 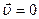и при учете только теплопроводности имеет вид

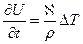. (7.8)

Так как 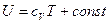, , 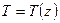то 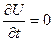и из (7.8) получаем, что

. (7.9)

Видно, что (7.6) удовлетворяет условию (7.9).

Пусть 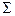– ограниченная поверхность (граничная поверхность тела или мысленно выделенная внутри жидкости поверхность), 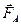– главный вектор, 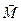– главный момент сил, действующих со стороны покоящейся как идеальной, так и вязкой жидкости на поверхность .

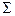Тогда

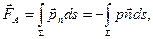(7.10)

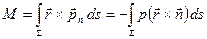. (7.11)

Рассмотрим твердое тело объема 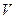, ограниченное поверхностью 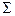, которое полностью погружено в покоящуюся жидкость (рис. 7.1). Найдем полную силу (7.10), действующую на это тело со стороны покоящейся жидкости или газа. Так как

,

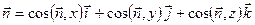то

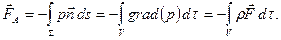
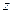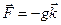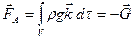Если – сила тяжести и ось направлена вверх, то , и , где 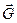– вес жидкости, заключенной в объеме 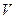. Таким образом, получен закон Архимеда: на тело, погруженное в покоящуюся тяжелую жидкость, со стороны жидкости действует подъемная сила, равная весу жидкости или газа, вытесненных телом. Эта сила называется силой Архимеда, или гидростатической подъемной силой. Сила Архимеда возникает из-за неравномерного распределения давления в жидкости (давление в тяжелой жидкости возрастает с глубиной).

Закон Архимеда также можно получить исходя из закона изменения количества движения

, или .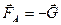

Система поверхностных сил, приложенных на поверхности 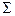, уравновешивается системой сил веса частиц среды внутри объема 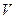. Поэтому совокупность системы сил, действующих на поверхности тела 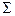, можно свести к одной силе, равной общему весу жидкости и приложенной в центре тяжести мысленно введенной внутрь поверхности 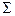массы жидкости с распределениями плотности и давления, удовлетворяющими уравнениям равновесия. Таким образом, линия действия силы Архимеда 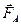проходит через центр тяжести массы вытесненной жидкости.

Если жидкость однородна, то центр тяжести вытесненной массы жидкости совпадает с центром тяжести вытесненного объема. В этом случае для тела, полностью погруженного в жидкость, точка приложения силы Архимеда, выделенная в теле, не зависит от ориентации тела. Однако для тел, погруженных в среду с неоднородной плотностью, сила Архимеда и ее линия действия зависят от положения тела в жидкости и от его ориентации (для частично погруженного в жидкость тела положение линии действия силы Архимеда относительно тела существенно зависит от ориентации тела).

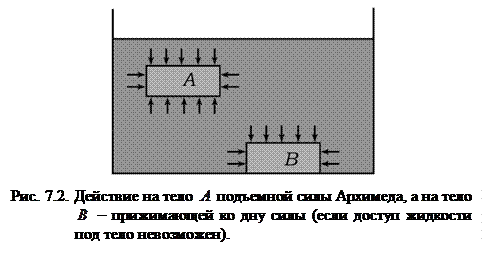
Надо сказать, что при выводе закона Архимеда существенным является предположение о замкнутости поверхности 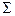соприкосновения тела с жидкостью. Если поверхность не будет замкнутой, то закон Архимеда не имеет места. На рис. 7.2 представлено расположение двух тел внутри жидкости, причем тело всей своей поверхностью граничит с жидкостью, а тело 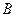своей нижней гранью плотно прижато ко дну сосуда. В этом случае на тело будет действовать выталкивающая сила; для тела 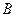подъемная сила исчезнет, а появится сила, прижимающая его ко дну (с этим связаны случаи, когда подводные лодки ложились на дно океана, теряли плавучесть и не могли всплыть).

Рассмотрим сосуд с жидкостью, в боковой стенке которого помещен цилиндр, который может вращаться без трения вокруг своей оси (рис. 7.3). Казалось бы, в таком случае должна возникнуть подъемная сила, действующая на часть цилиндра, находящуюся в воде, и под действием этой силы цилиндр должен начать вращаться. Однако этого не происходит (в этом заключается парадокс Жуковского), т.к. равнодействующая сил, действующих со стороны воды на цилиндр, проходит не через центр объема вытесненной жидкости, а через ось цилиндра (т.к. давление в каждой точке поверхности цилиндра направлено по нормали к ней).

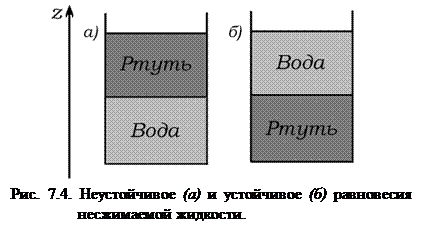
Рассмотрим вопрос об устойчивости равновесия несжимаемой жидкости. Пусть, например, имеются два сосуда, и две различных по плотности жидкости (например, вода и ртуть). Тогда с точки зрения уравнений равновесия тяжелой жидкости, возможны два состояния равновесия, изображенные на рис. 7.4. Выясним, какое из них является устойчивым.

Равновесие называют устойчивым, если после произвольного малого перемещения система стремится возвратиться в прежнее состояние равновесия. Равновесие будет неустойчивым, если найдется такое малое перемещение всей системы или ее части, после которого система стремится еще более удалиться от положения равновесия. Равновесие будет безразличным, если в системе можно произвести любое малое перемещение, не нарушая равновесия.

Очевидно, что состояние равновесия, изображенное на рис. 7.4, а, будет неустойчивым, т.к. частица ртути, смещенная в слой воды, в силу того, что действующая на нее архимедова сила будет меньше действующей на нее силы тяжести, начнет опускаться вниз. Равновесие же, изображенное на рис. 7.4, б, будет устойчивым.

В качестве примера безразличного равновесия можно привести равновесие в некоторой однородной жидкости полностью погруженного в нее шарика из материала с плотностью, равной плотности окружающей его жидкости. В таком равновесии внутри слоя однородной жидкости может находиться и полый шарик, если его средняя по всему объему плотность будет равна плотности окружающей жидкости.

Таким образом, необходимое условие устойчивости состояния равновесия несжимаемой жидкости в поле сил тяжести заключается в том, чтобы плотность среды увеличивалась с глубиной (или оставалась постоянной для случая безразличного равновесия), т.е. .

Центр масс погруженного в жидкость тела 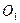может не совпадать с центром объема вытесненной жидкости 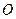(рис. 7.5). Это несовпадение имеет большое значение для устойчивого плавания тел, погруженных в жидкость (в кораблестроении используется термин остойчивость). На рис. 7.5, а изображено поперечное сечение некоторого тела, погруженного в воду, при этом его центр тяжести, к которому приложена сила тяжести 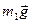(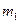– масса погруженного тела), находится ниже точки приложения Архимедовой силы. Естественно, что при боковом наклоне такого тела момент указанной пары сил будет возвращать его в вертикальное положение.

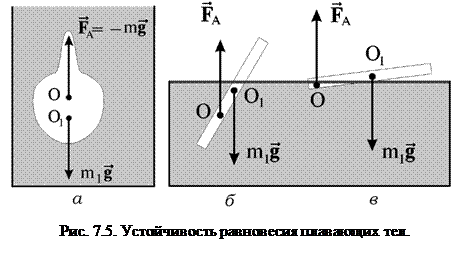Для тел, плавающих на поверхности жидкости, центр их тяжести всегда будет расположен выше центра объема, погруженного в жидкость, и остойчивость плавания, например, корабля достигается выбором соответствующей формы корабля и его загрузки. Хорошо известно, что, например, карандаш, никогда не плавает на поверхности жидкости в вертикальном положении. Пара сил, возникающая при неизбежном случайном отклонении карандаша от вертикали, немедленно роняет его на поверхность (рис. 7.5 б, в). Устойчиво будет плавать “горизонтальный карандаш”. При его малейшем наклоне (рис. 7.5 в) он будет возвращаться в исходное горизонтальное положение.

Пусть имеется сосуд, который вращается вокруг вертикальной оси 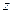с постоянной угловой скоростью 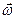. Требуется определить форму свободной поверхности налитой в сосуд жидкости при условии, что она находится в покое по отношению к сосуду.

Тогда уравнение (7.1) перепишем в виде

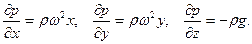
Общее их решение имеет вид:

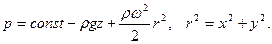
Для точки 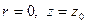на свободной поверхности имеем 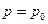, поэтому 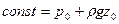, откуда

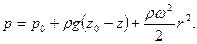
Уравнение свободной поверхности жидкости, на которой 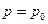, имеет вид

,

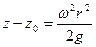т.е. параболоид вращения. Аналогичную форму будут иметь и все другие изобарические поверхности. Вектор 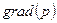направлен по нормали к соответствующим параболоидам.

Если в жидкость поместить частицы разной плотности, то в результате вращения частицы с плотностью, меньшей плотности вращающейся жидкости, под действием силы Архимеда, обусловленной силой тяжести и центробежной силой, поднимутся вверх и соберутся вблизи оси вращения; частицы же, плотность которых больше плотности жидкости, опустятся вниз и расположатся у стенок сосуда.

Замечание. Если сосуд вращать с угловым ускорением, то появится дополнительная составляющая сил инерции, перпендикулярная радиусу 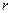сосуда и равная 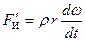. Эта сила не будет потенциальной, поскольку ее работа, например, вдоль окружности радиуса 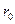отлична от нуля и равна 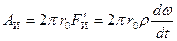. В силу этого равновесие жидкости невозможно: жидкость будет вращаться относительно цилиндра, причем распределение скоростей и давлений можно получить, рассматривая уравнения гидродинамики, в которых должны быть учтены силы вязкости.