Пусть имеется однородная несжимаемая жидкость, движущаяся в поле сил тяжести. Направим ось 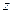 вертикально вверх, тогда
вертикально вверх, тогда 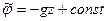 и интеграл Бернулли примет вид
и интеграл Бернулли примет вид
 . (7.19)
. (7.19)
Выбрав на линии тока точку с координатой 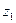 , можно определить постоянную
, можно определить постоянную 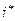 по значениям параметров
по значениям параметров 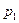 и
и 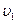 в этой точке:
в этой точке:
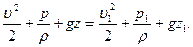 (7.20)
(7.20)
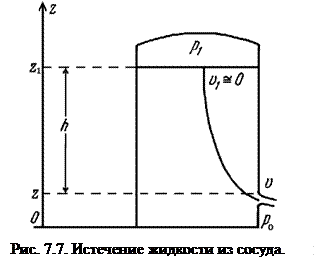
 Определим скорость истечения несжимаемой жидкости из сосуда (рис. 7.7). Предположим, что сосуд достаточно велик, а отверстие мало. В этом случае можно считать в течение малого времени течение установившимся.
Определим скорость истечения несжимаемой жидкости из сосуда (рис. 7.7). Предположим, что сосуд достаточно велик, а отверстие мало. В этом случае можно считать в течение малого времени течение установившимся.
Выберем некоторую линию тока (все линии тока начинаются, очевидно, на свободной поверхности, где 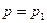 и
и 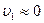 ). На свободной поверхности вытекающей струи
). На свободной поверхности вытекающей струи 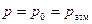 . Будем приближенно считать, что на выходе из сосуда давление внутри струи всюду равно
. Будем приближенно считать, что на выходе из сосуда давление внутри струи всюду равно 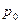 , а величина скорости равна
, а величина скорости равна 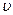 . Тогда
. Тогда
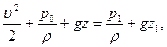
откуда
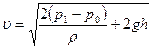 . (7.21)
. (7.21)
 |
Если давление на свободной поверхности в жидкости в сосуде равно атмосферному, то из (7.21) получим формулу
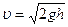 ,
,
которая была получена опытным путем Е. Торричелли (1608 – 1674) и носит его имя.
Если создать очень высокое избыточное давление, например, 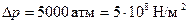 , то скорость истечения воды, согласно (7.21), будет
, то скорость истечения воды, согласно (7.21), будет 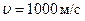 . Если такую струю направить на какой-либо твердый материал, то его поверхность будет подвержена гидродинамическому давлению
. Если такую струю направить на какой-либо твердый материал, то его поверхность будет подвержена гидродинамическому давлению 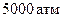 . Такое давление в ряде случаев превосходит предел прочности некоторых материалов, и они будут разрушаться под действием струи. Со второй половины 80-х годов получило развитие новое направление в обработке материалов – гидрорезание. В этой технологии водяной нож – высокоскоростная струя воды с диаметром иглы – легко режет материалы толщиной в несколько сантиметров со скоростью резания несколько десятков сантиметров в минуту. Для увеличения производительности гидрорезания в струю добавляют абразивный порошок.
. Такое давление в ряде случаев превосходит предел прочности некоторых материалов, и они будут разрушаться под действием струи. Со второй половины 80-х годов получило развитие новое направление в обработке материалов – гидрорезание. В этой технологии водяной нож – высокоскоростная струя воды с диаметром иглы – легко режет материалы толщиной в несколько сантиметров со скоростью резания несколько десятков сантиметров в минуту. Для увеличения производительности гидрорезания в струю добавляют абразивный порошок.

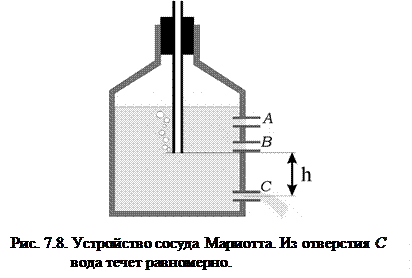
Рассмотрим сосуд с узким горлом, через герметичную пробку в горловине которого введена стеклянная трубочка, сообщающаяся с атмосферой (рис. 7.8). Такая конструкция сосуда позволяет обеспечить постоянную скорость вытекания жидкости из сосуда, несмотря на понижение ее уровня (до отверстия 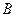 на рис. 7.8). Скорость вытекания определяется по формуле Торричелли, где
на рис. 7.8). Скорость вытекания определяется по формуле Торричелли, где  – высота нижнего конца трубки над отверстием (на уровне пробки
– высота нижнего конца трубки над отверстием (на уровне пробки 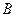 ). Скорость вытекания легко регулируется вертикальным перемещением трубки.
). Скорость вытекания легко регулируется вертикальным перемещением трубки.
Проанализируем, почему такое происходит. При открытии отверстия 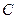 , прежде всего, выливается вода из стеклянной трубки; уровень жидкости внутри нее опускается до конца трубки. При дальнейшем вытекании опускается уже уровень воды в сосуде и через стеклянную трубку входит наружный воздух. Он просачивается пузырьками через воду и собирается над ней в верхней части сосуда. Теперь на всем уровне пробки
, прежде всего, выливается вода из стеклянной трубки; уровень жидкости внутри нее опускается до конца трубки. При дальнейшем вытекании опускается уже уровень воды в сосуде и через стеклянную трубку входит наружный воздух. Он просачивается пузырьками через воду и собирается над ней в верхней части сосуда. Теперь на всем уровне пробки 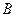 давление равно атмосферному. Значит, вода из отверстия
давление равно атмосферному. Значит, вода из отверстия 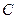 вытекает лишь под давлением слоя воды
вытекает лишь под давлением слоя воды 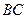 . А так как толщина слоя
. А так как толщина слоя 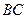 остается постоянной (до тех пор, пока уровень жидкости в сосуде не опустится до пробки
остается постоянной (до тех пор, пока уровень жидкости в сосуде не опустится до пробки 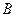 ), то жидкость из отверстия
), то жидкость из отверстия 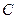 вытекает с одной и той же скоростью.
вытекает с одной и той же скоростью.
 |
Если же отверстие 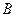 открыть, то жидкость через него вовсе не будет вытекать, независимо от того, открыто или закрыто отверстие
открыть, то жидкость через него вовсе не будет вытекать, независимо от того, открыто или закрыто отверстие 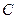 (если отверстие
(если отверстие 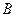 настолько мало, что шириной его можно пренебречь, – иначе вода будет вытекать из него под давлением тонкого слоя воды толщиной в ширину отверстия; если же в отверстие
настолько мало, что шириной его можно пренебречь, – иначе вода будет вытекать из него под давлением тонкого слоя воды толщиной в ширину отверстия; если же в отверстие 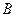 вставить изогнутую трубочку, то отверстие
вставить изогнутую трубочку, то отверстие 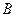 может быть и не очень мало). В самом деле, здесь изнутри и снаружи сосуда давление равно атмосферному, и ничто не побуждает воду вытекать.
может быть и не очень мало). В самом деле, здесь изнутри и снаружи сосуда давление равно атмосферному, и ничто не побуждает воду вытекать.
Можно открыть пробку  выше нижнего конца трубки. В этом случае не только вода не вытекает из сосуда, но в сосуд начинает входить наружный воздух, т.к. внутри этой части сосуда давление воздуха меньше, чем атмосферное давление снаружи.
выше нижнего конца трубки. В этом случае не только вода не вытекает из сосуда, но в сосуд начинает входить наружный воздух, т.к. внутри этой части сосуда давление воздуха меньше, чем атмосферное давление снаружи.

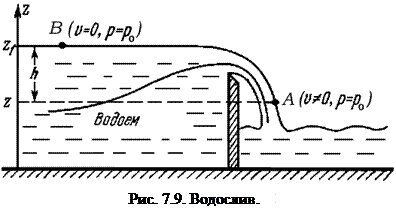
Определим скорость на свободной поверхности жидкости, перетекающей через вертикальную стенку (рис. 7.9). Предположим, что объем водоема очень велик, и можно считать, что уровень жидкости далеко от водослива практически не меняется и равен 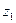 . Движение можно считать установившимся.
. Движение можно считать установившимся.
Свободная поверхность жидкости является поверхностью тока, на которой давление равно атмосферному 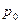 , а скорость в точках водоема, далеких от стенки, равна нулю. Из интеграла Бернулли следует, что
, а скорость в точках водоема, далеких от стенки, равна нулю. Из интеграла Бернулли следует, что
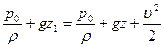 ,
,
откуда 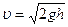 , где
, где 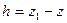 ,
, 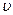 – скорость в произвольной точке
– скорость в произвольной точке  на свободной поверхности жидкости с координатой
на свободной поверхности жидкости с координатой 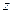 .
.
 |
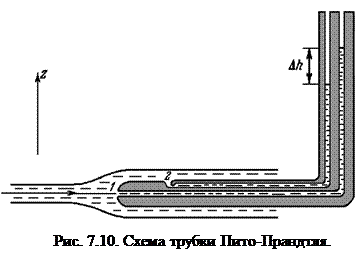
Скорость течения жидкости измеряют обычно с помощью трубки Пито – Прандтля, которая представляет собой тонкое вытянутое цилиндрическое тело со скругленной передней частью (рис. 7.10). При такой форме трубка слабо искажает распределение скоростей в потоке. Для измерения скорости трубку Пито – Прандтля помещают в жидкость и располагают ее вдоль потока. На теле трубки пито – Прандтля имеются отверстия, через которые по каналам, расположенным внутри тела трубки, жидкость может поступать в два колена манометра. Одно из отверстий расположено в передней точке трубки Пито - Прандтля (точка 1). Другое – на ее цилиндрической части, на достаточном удалении от первого (точка 2), так, чтобы искажение поля скоростей за счет обтекания скругленного конца трубки Пито – Прандтля можно было не учитывать при рассмотрении течения вблизи второго отверстия. При обтекании трубки потоком жидкости передняя точка 1 будет критической точкой, в ней скорость 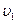 будет равна нулю, а давление
будет равна нулю, а давление 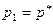 . Давление в критической точке иногда называют полным давлением или давлением торможения. В точке 2 скорость и давление приближенно равны скорости и давлению в набегающем потоке при отсутствии в нем трубки,
. Давление в критической точке иногда называют полным давлением или давлением торможения. В точке 2 скорость и давление приближенно равны скорости и давлению в набегающем потоке при отсутствии в нем трубки,  и
и 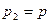 .
.
 |
Применив интеграл Бернулли к точкам 1 и 2, лежащим на одной линии тока, будем иметь
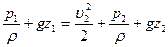 ,
,
где 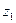 и
и 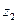 – вертикальные координаты точек 1 и 2. Пренебрегая членом
– вертикальные координаты точек 1 и 2. Пренебрегая членом  ввиду малой толщины трубки, получим
ввиду малой толщины трубки, получим
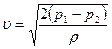 .
.
Разность давлений 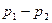 равна, очевидно, удельному весу жидкости, используемой в манометре
равна, очевидно, удельному весу жидкости, используемой в манометре 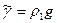 , умноженному на разность
, умноженному на разность 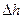 высот уровней жидкости в вертикальных коленах манометра, поэтому, если
высот уровней жидкости в вертикальных коленах манометра, поэтому, если  , то
, то
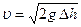 .
.

Рассмотрим зависимость давления от скорости вдоль линии тока. Возьмем на данной линии тока две точки с вертикальными координатами 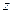 и
и 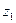 ; давления и величины скоростей – соответственно
; давления и величины скоростей – соответственно 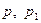 и
и 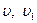 .
.
Из интеграла Бернулли получим
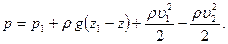 (7.22)
(7.22)
Видно, что давления в двух точках на линии тока, как и в гидростатике, отличаются на величину 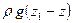 , вызванную разностью уровней, и, кроме того, на величину
, вызванную разностью уровней, и, кроме того, на величину 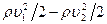 , связанную с разностью скоростей в этих точках.
, связанную с разностью скоростей в этих точках.
Назовем в (7.22) член 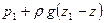 гидростатическим давлением, а член
гидростатическим давлением, а член 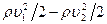 , зависящий от скорости, динамическим давлением.
, зависящий от скорости, динамическим давлением.
Во многих случаях, например, при полете самолетов, динамическая подъемная сила оказывается во много раз больше гидростатической. При движении же больших по объему тел с малыми скоростями, роль динамических давлений в создании подъемной силы незначительна. Подъемная сила динамической природы удерживает суда над водой при движении на подводных крыльях и при скольжении (глиссировании) по поверхности воды судов, имеющих днище, смоченная часть которых имеет “плоскодонную” форму.
Рассмотрим для примера обтекание несимметричного профиля крыла горизонтальным поступательным потоком воздуха с постоянной не слишком большой скоростью на бесконечности, равной 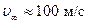 (рис. 7.11). Для таких скоростей при вычислении давления в установившемся движении воздух с большой точностью можно считать несжимаемой жидкостью.
(рис. 7.11). Для таких скоростей при вычислении давления в установившемся движении воздух с большой точностью можно считать несжимаемой жидкостью.
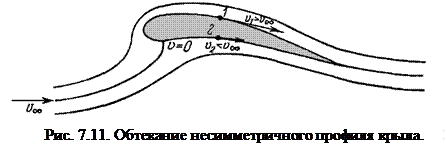 |
При обтекании несимметричного профиля крыла скорость на его верхней поверхности больше, чем на нижней, а давление, как это следует из интеграла Бернулли, наоборот, больше на нижней поверхности. Предположим, что скорости в точках 1 и 2 на верхней и нижней поверхностях крыла отличаются на величину порядка 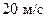 . Например, в точке 1 скорость равна
. Например, в точке 1 скорость равна 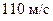 , а в точке 2 –
, а в точке 2 – 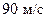 . Тогда, т.к. плотность воздуха при обычных условиях
. Тогда, т.к. плотность воздуха при обычных условиях 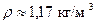 , разница в давлениях за счет разницы скоростей в точках 1 и 2 будет около
, разница в давлениях за счет разницы скоростей в точках 1 и 2 будет около 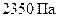 . В то же время разница гидростатических давлений в этих точках при вертикальном размере крыла порядка
. В то же время разница гидростатических давлений в этих точках при вертикальном размере крыла порядка 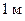 будет всего около
будет всего около 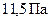 .
.

Рассмотрим движение несжимаемой жидкости в тонкой трубке переменного поперечного сечения (рис. 7.12).
Будем считать, что течение в такой трубке одномерное, т.е. скорости жидкости в различных точках каждого сечения 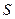 приблизительно одинаковы и могут отличаться при установившемся движении только при переходе от одного сечения к другому. В силу неразрывности течения через каждое поперечное сечение в единицу времени должен проходить одинаковый объем жидкости, т.е. вдоль трубки верно равенство
приблизительно одинаковы и могут отличаться при установившемся движении только при переходе от одного сечения к другому. В силу неразрывности течения через каждое поперечное сечение в единицу времени должен проходить одинаковый объем жидкости, т.е. вдоль трубки верно равенство
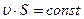 .
.
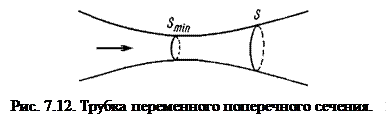 |
Видно, что с уменьшением сечения 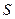 скорость растет. В минимальном сечении
скорость растет. В минимальном сечении 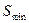 скорость имеет наибольшее значение
скорость имеет наибольшее значение 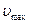 . Из интеграла Бернулли (при
. Из интеграла Бернулли (при 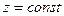 ) имеем
) имеем
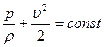 . (7.23)
. (7.23)
Следовательно, с уменьшением сечения 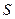 давление
давление 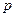 уменьшается. В этом заключается принцип, впервые высказанный Д. Бернулли в 1726 г.: “в струе воды или воздуха давление велико, если скорость мала, и давление мало, если скорость велика”, который впоследствии получил название принципа Бернулли.
уменьшается. В этом заключается принцип, впервые высказанный Д. Бернулли в 1726 г.: “в струе воды или воздуха давление велико, если скорость мала, и давление мало, если скорость велика”, который впоследствии получил название принципа Бернулли.
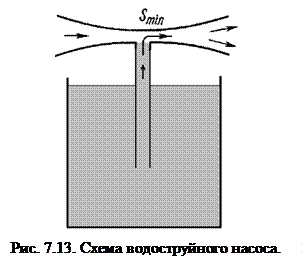 |
Это свойство используется, например, в водоструйных и пароструйных насосах, в разбрызгивателях (рис. 7.13). При подаче воздуха в трубку переменного поперечного сечения в области минимального сечения  может возникнуть давление меньшее, чем давление в сосуде. Под действием образовавшегося перепада давлений жидкость из сосуда поднимается по трубке, и вместе с потоком воздуха капли жидкости выбрасываются в окружающую среду.
может возникнуть давление меньшее, чем давление в сосуде. Под действием образовавшегося перепада давлений жидкость из сосуда поднимается по трубке, и вместе с потоком воздуха капли жидкости выбрасываются в окружающую среду.
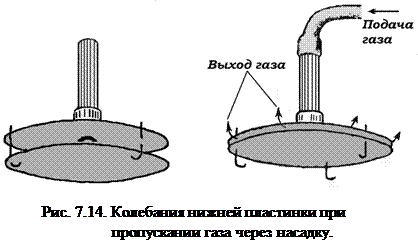
Если через насадку, изображенную на рис. 7.14, пропускать сильную струю газа, то нижняя подвижная пластина начинает колебаться вверх и вниз, ударяясь о верхнюю. Скорость газа у края насадки уже мала. Как было указано, уравнение Бернулли можно применить ко всему потоку в целом. Но линии тока расходятся от центра насадки к краям, т.е. скорость от центра к краям падает, а значит, давление растет. Так как давление у края насадки равно атмосферному, то везде ближе к центру (где линии тока гуще), оно меньше атмосферного. Избыток внешнего (атмосферного) давления поднимает нижнюю пластину, перекрывая поток газа. Вследствие этого давление газа в подводящей трубке растет, избыток внешнего давления исчезает, пластина падает и процесс повторяется.
 |
С тем, что с уменьшением сечения трубки 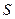 давление
давление 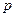 на ее стенки уменьшается, приходится также считаться при проходе двух кораблей на близком расстоянии друг от друга. Дело в том, что в этом случае между кораблями образуется узкий канал, в котором роль стенок играют корпуса кораблей (в обыкновенном канале стенки неподвижны, а движется вода; здесь же, наоборот: неподвижна вода, а движутся стенки – корпуса кораблей). Таким образом, бока кораблей, обращенные друг к другу, испытывают со стороны воды меньшее давление, чем наружные части судов. В результате под напором наружной воды корабли должны двинуться друг к другу, что может привести к столкновению (одно из таких крупных столкновений произошло в 1912 г. между океанским пароходом “Олимпик” и крейсером “Гаук”). Наконец, втягивающее действие быстро движущегося поезда также объясняется принципом Бернулли: поезд при скорости
на ее стенки уменьшается, приходится также считаться при проходе двух кораблей на близком расстоянии друг от друга. Дело в том, что в этом случае между кораблями образуется узкий канал, в котором роль стенок играют корпуса кораблей (в обыкновенном канале стенки неподвижны, а движется вода; здесь же, наоборот: неподвижна вода, а движутся стенки – корпуса кораблей). Таким образом, бока кораблей, обращенные друг к другу, испытывают со стороны воды меньшее давление, чем наружные части судов. В результате под напором наружной воды корабли должны двинуться друг к другу, что может привести к столкновению (одно из таких крупных столкновений произошло в 1912 г. между океанским пароходом “Олимпик” и крейсером “Гаук”). Наконец, втягивающее действие быстро движущегося поезда также объясняется принципом Бернулли: поезд при скорости 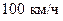 увлекает близстоящего человека с силой порядка
увлекает близстоящего человека с силой порядка 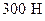 .
.
 2014-02-02
2014-02-02 2329
2329
