Жидкости и газа. Интеграл Бернулли

Общая теория установившихся движений идеальных

Рассмотрим уравнение движения Эйлера в форме Громеки – Лемба

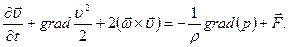(7.12)

Так как мы рассматриваем установившееся движение, то

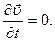(7.13)

Будем считать также, что внешние массовые силы обладают потенциалом, т.е.

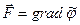. (7.14)

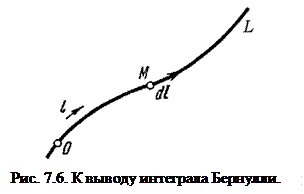
Рассмотрим в потоке жидкости некоторую произвольную линию 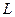и пусть 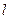– введенное вдоль нее направление отсчета заданной длины (начиная от некоторой точки 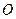). Пусть 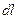– элемент касательной к линии 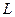в произвольной точке 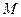(рис. 7.6).

Проектируя уравнение (7.12) на направление касательной к линии 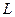в произвольной точке 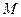с учетом сделанных предположений (7.13) и (7.14), получим

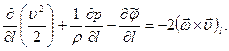(7.15)

Здесь мы учли, что проекция градиента на некоторое направление равна производной, взятой по этому направлению.

Вдоль данной линии 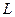плотность и давление являются функциями длины дуги 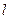. Эти функции различны для разных линий 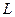, т.е.

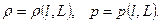
Очевидно, что вдоль данной линии 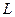плотность 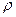всегда можно считать функцией давления, т.е. 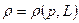, и всегда можно ввести функцию давления :

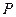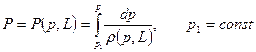(7.16)

так, что

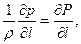
причем это равенство и функция давления 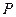имеют место только для данной линии 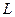. Очевидно, что функция давления определена только с точностью до аддитивной постоянной, которая связана с выбором 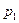и может зависеть от .

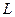В случае баротропных процессов, если известна зависимость 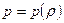, так введенная функция давления 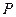легко вычисляется и не зависит от линии 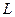, если 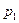не зависит от 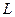. Так, для однородной несжимаемой жидкости

.

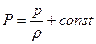Для изотермических процессов в совершенном газе, когда ,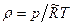

.

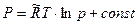В случае небаротропных процессов 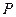зависит от .

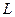Перепишем (7.15) в виде

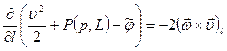. (7.17)

Пусть теперь 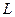– линия тока. Тогда т.к. перпендикулярен к линии тока, а также перпендикулярен вихревой линии (однако в общем случае функции 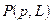на линии тока и на вихревой линии различны), то . Таким образом, вдоль линий тока и вихревых линий имеем

,

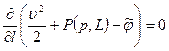т.е.

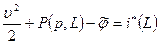. (7.18)

Если функция давления 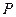известна, то (7.18) является первым интегралом уравнений движения идеальной жидкости и называется интегралом Бернулли.

Уравнение (7.18) в виде

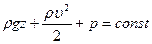
было выведено Даниилом Бернулли в 1738 году.

Если функция давления 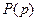и значение постоянной 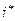вдоль данной линии тока или вихревой линии известны, то, пользуясь интегралом Бернулли, можно в любой точке линии тока или вихревой линии, зная скорость, найти давление, и наоборот. Ясно, что для определения постоянной 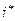достаточно знать значения характеристик движения жидкости, входящих в левую часть интеграла Бернулли, только в одной точке на линии тока или вихревой линии.

При наличии баротропии постоянная интеграла Бернулли одинакова для части или всей массы жидкости и не зависит от линии тока или вихревой линии, если векторное произведение в этой массе жидкости равно нулю. Это может быть в тех случаях, когда:

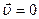- (гидростатика),

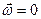- (движение потенциально),

- вектор вихря 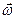коллинеарен вектору скорости .

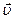Последний случай не может иметь место при движении твердого тела и плоскопараллельных движениях жидкости, в которых 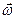ортогонально 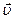. Для деформируемых тел случай, когда 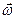параллельно 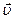, может иметь место. Например, если непрерывное поле скоростей задается формулами

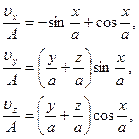
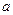где и – постоянные, то можно легко показать, что 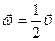, а значит, в заданном поле скоростей линии тока совпадают с вихревыми линиями.

Заметим также, что постоянная 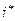в интеграле Бернулли одна и та же на таких линиях тока, которые начинаются или проходят через область, где все характеристики движения одинаковы.